不稳定翘曲导致零部件挫曲。三个收缩变量中的每一个对总变形的贡献都不能再假设是线性的。
这种情况下使用所谓的敏感度分析。该功能仅用于中性面分析技术。
敏感度分析的目的是为已知的收缩变化确定载荷因子变化。载荷因子表示实际上用多大的系数应用了载荷,在收缩分析中,它们是零件内部载荷,零件翘曲变得不稳定,从而造成挫曲。小于 1 的载荷因子表示实际载荷足以导致零件挫曲。大于 1 的载荷因子表示翘曲稳定,因为挫曲的初始阶段已确定在高于实际载荷的载荷等级上。
假设收缩组成可以单独变化,而载荷因子 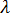 可视为这些组成的函数,即
可视为这些组成的函数,即 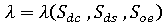
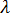 可视为这些组成的函数,即
可视为这些组成的函数,即 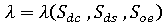
为解决翘曲问题,我们希望知道该更改哪个分量来提高载荷因子,也就是说使翘曲稳定。一种方法是相对于每个组成执行 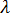 局部衍生。很抱歉,无法通过解析法完成,因为没有已知的函数能够将
局部衍生。很抱歉,无法通过解析法完成,因为没有已知的函数能够将 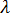 与组成相关联。替代方法是对偏导数取近似。
与组成相关联。替代方法是对偏导数取近似。
假设挫曲分析使用总收缩输出载荷因子 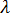 。现在,将其中一个收缩组成提高一定的数值
。现在,将其中一个收缩组成提高一定的数值 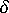 即,给出一个新的总收缩 S'。例如,如果加大收缩不均分量,则有:
即,给出一个新的总收缩 S'。例如,如果加大收缩不均分量,则有: 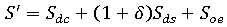
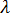 。现在,将其中一个收缩组成提高一定的数值
。现在,将其中一个收缩组成提高一定的数值 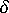 即,给出一个新的总收缩 S'。例如,如果加大收缩不均分量,则有:
即,给出一个新的总收缩 S'。例如,如果加大收缩不均分量,则有: 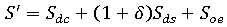
如果此 S' 值用于挫曲分析以获得新的载荷因子 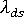 ,则相对于不同收缩组成的
,则相对于不同收缩组成的 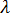 衍生大致如下:
衍生大致如下: 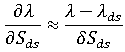
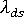 ,则相对于不同收缩组成的
,则相对于不同收缩组成的 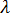 衍生大致如下:
衍生大致如下: 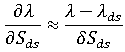
如下图所示:
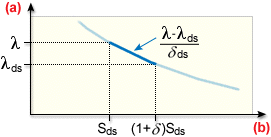
载荷因子作为收缩的函数
.(a) 载荷因子,(b) 收缩
值 (1 + 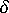 ) 被称为灵敏度因子,它由程序输入。
) 被称为灵敏度因子,它由程序输入。
上述方法只适用于一个单元。对于实际零件,每个单元都有一个 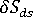 值。为处理这种情况,各种不同的单元变化被合并成一种形式的收缩变化。这些更改的标准将用于单元收缩以获取单一值,并将在分析日志中作为收缩更改标准进行报告。
值。为处理这种情况,各种不同的单元变化被合并成一种形式的收缩变化。这些更改的标准将用于单元收缩以获取单一值,并将在分析日志中作为收缩更改标准进行报告。
这个范数定义为: 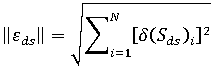
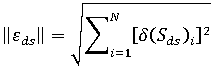
其中 N 是模型中单元的数量。
采用相似方法计算冷却不均和取向效应变量的载荷因子的灵敏度。
这时,收缩更改标准是每个单元的收缩更改平方和,并用于翘曲挫曲的敏感度分析。