3D 流动结果基于以下考虑事项。
要模拟模具型腔内的流动,需要将动量、质量和能量守恒方程离散成有限元。
通过以下等式定义:
流体的质量守恒
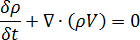
其中
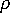 为聚合物密度
为聚合物密度 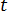 为时间
为时间 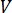 为速度矢量
为速度矢量
动量守恒
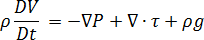
其中
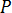 为压力
为压力  为粘滞应力张量
为粘滞应力张量 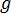 重力加速度矢量
重力加速度矢量
能量守恒
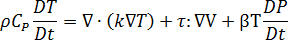
其中
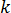 为聚合物热导率
为聚合物热导率 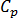 为熔体的比热容
为熔体的比热容 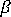 为聚合物膨胀率,定义如下
为聚合物膨胀率,定义如下
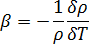
对于压力-速度(动量和质量守恒)解决方案。
- 将通过标准有限元方法求解方程。这包括所有工艺阶段中的材料可压缩性。
- 将同时求解柱体单元和四面体单元。
- 每个柱体单元的阴影中的所有四面体节点都将被施加相同压力。
- 在柱体单元中,将假定有 1D 流动且使用 Hele-Shaw 逼近。
- 在四面体单元中,将执行完整的斯托克斯解决方案(如果惯性选项处于选定状态,则为纳维-斯托克斯方程)。
对于温度(能量守恒)解决方案
- 将通过标准有限元方法求解方程。
- 对于柱体单元和四面体单元,将包括剪切热、对流、传导和压缩加热项。
- 在柱体单元中,近似沿柱体长度的可忽略传导。对于柱体单元中的温度守恒,我们在每个柱体层内进行逆风处理。
- 求解温度方程时,我们将时间段分割成许多较短的子段,以提高精确度。
在每个时间段中,我们在温度和压力-速度方程之间进行迭代,直到达到收敛。