Hyperelastisch

Definiert Materialeigenschaften zur Verwendung in vollständig nichtlinearen (d. h. mit großer Dehnung und Drehung) hyperelastischen Analysen von gummiähnlichen Materialien (Elastomere) für isoparametrische Volumenkörperelemente.

• Die verallgemeinerte Mooney-Rivlin-Dehnungsenergie kann wie folgt ausgedrückt werden:

  

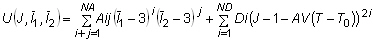
  Dabei si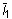nd und 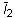die ersten bzw. zweiten distortionalen Dehnungsinvarianten. J = det F ist die Determinante des Verformungsgradienten, und 2D1 = K und 2 (A10 + A01) = G bei kleinen Dehnungen, bei denen K das Massenmodul ist. Das Modell wird zu einem Mooney-Rivlin-Material reduziert, wenn NA = 1, und zu einem Neo-Hookschen Material, wenn NA = 1 und A01 = 0,0. Für Neo-Hooksche oder Mooney-Rivlin-Materialien ist keine Fortsetzungseingabe erforderlich. 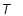ist die aktuelle Temperatur, und 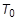ist die anfängliche Temperatur.

• Die verallgemeinerte Ogden-Dehnungsenergie kann wie folgt ausgedrückt werden:

  

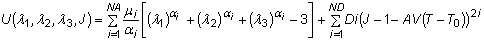
  Dabei si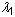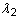nd , und 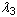Hauptstreckungen. J = det F ist die Determinante des Verformungsgradienten, und 2D1 = K bei kleinen Dehnungen, bei denen K das Massenmodul ist. 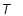ist die aktuelle Temperatur, und 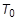ist die anfängliche Temperatur.

  Die Vorgabe für D1 ist 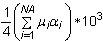. Die Vorgabe für D2 bis D4 ist null.

• Hyperelastische Materialien weisen ein vollständig inkompressibles oder nahezu inkompressibles Verhalten auf. Vollständige Inkompressibilität ist zurzeit nicht verfügbar, während nahezu inkompressibles Verhalten mit einem großen D1-Wert simuliert werden kann.

Nachdem Sie Hyperelastisch aus der Dropdown-Liste Typ ausgewählt haben, sind die folgenden Materialbereiche verfügbar: Hyperelastisch und Funktion experimenteller Daten.

• Hyperelastisch

  

  

  

  

  

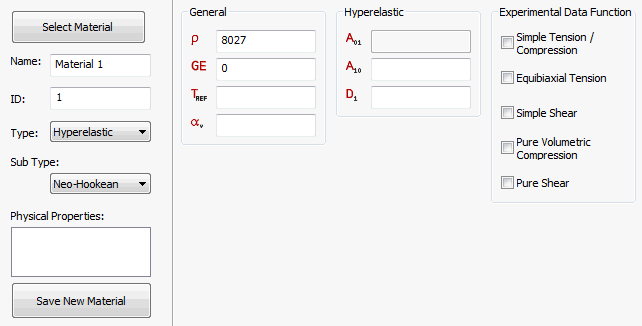
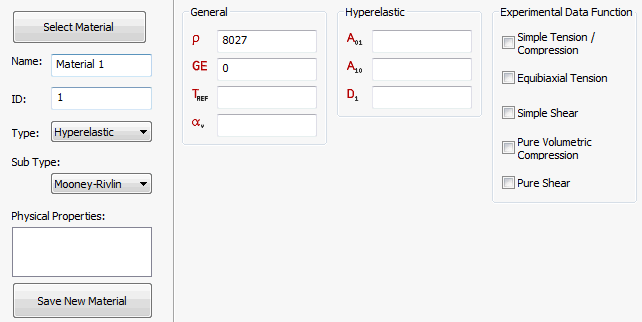
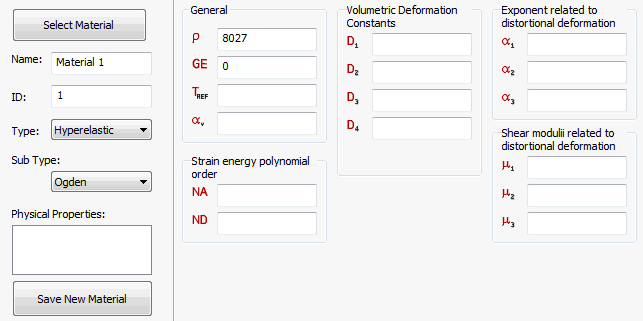
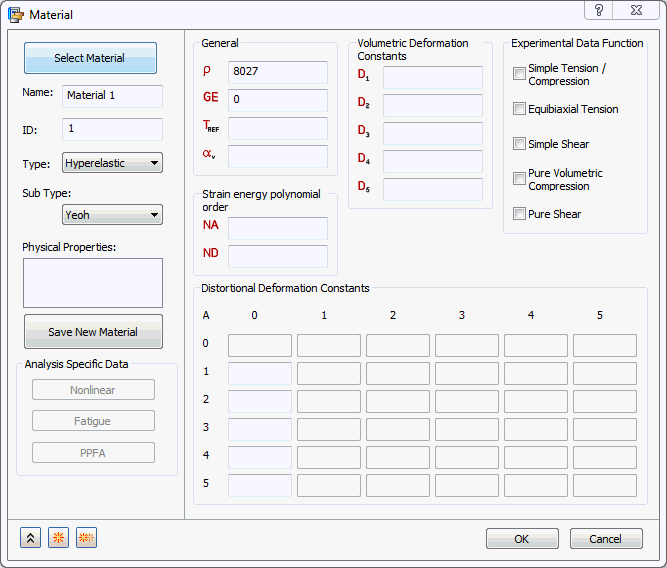
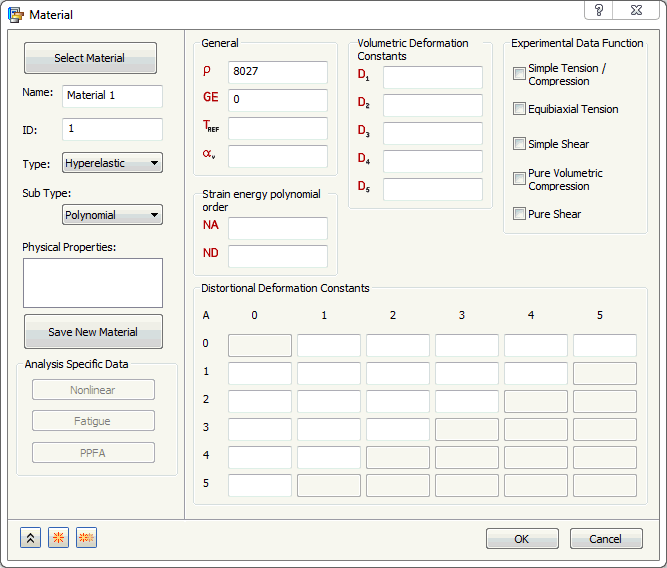
  • Für Untertyp stehen die Optionen Neo-Hookean, Mooney-Rivlin, Ogden, Yeoh und Polynom zur Auswahl, wie in den Abbildungen oben gezeigt. Jeder Typ enthält spezifische zu definierende Materialkonstanten.
  • Die Massendichte, RHO, wird verwendet, um automatisch die Masse für alle strukturellen Elemente zu berechnen.
  • Um den Dämpfungskoeffizienten GE zu ermitteln, multiplizieren Sie das kritische Dämpfungsverhältnis C/C0 mit 2,0. Wenn für die Materialstrukturdämpfung keine dominante Frequenz definiert ist (siehe Abschnitt Dämpfungen), dann wird GE in transienten Antwortanalysen ignoriert.
  • TREF wird nur als Referenztemperatur für die Berechnung der thermischen Last in linearen Lösungen verwendet. Wenn eine Ausgangstemperaturlast angegeben ist, wird TREF ignoriert.
  • Sie können die thermischen Ausdehnungskoeffizienten, die Massendichte, den Materialdämpfungskoeffizienten und Referenzmaterialien definieren.
• Funktion experimenteller Daten
  • Aij und Di werden aus der Kleinste-Quadrate-Approximation der experimentellen Daten ermittelt. Eines oder mehrere der vier Experimente (einfacher Spannungsdruck, äquibiaxiale Spannung, einfache Scherung, reine Scherung, reiner volumetrischer Druck) können verwendet werden, um Aij zu ermitteln. Di können Sie aus reinen volumetrischen Druckdaten (TABD) ermitteln. Wenn alle TAB1 bis TAB4 leer sind, muss Aij vom Benutzer angegeben werden. Aus einer der Tabellen prognostizierte Parameterwerte ersetzen die manuelle Eingabe der Parameter.
  • Wenn ND = 1 und ein D1-Wert ungleich null aus experimentellen Daten eines reinen volumetrischen Drucks bereitgestellt oder ermittelt wird, dann berücksichtigt die Parameterprognose der Materialkonstanten Aij die Kompressibilität in den Fällen, in denen einfacher Zug/Druck, äquibiaxiale Spannung und allgemeine biaxiale Verformung vorhanden sind. Andernfalls wird bei der Prognose der Materialkonstanten die vollständige Inkompressibilität angenommen.

    

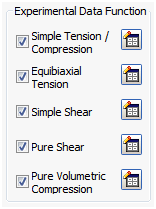
    • Tabellensymbol: Ermöglicht es Ihnen, eine Funktion experimenteller Daten aus physischen Tests zu definieren. Sie können Tabellen für Einfacher Zug/Druck, Äquibiaxiale Spannung, Einfache Scherung, Reine Scherung und Reiner volumetrischer Druck definieren.
    • Einfacher Zug/Druck: Daten für die Prognose der Materialkonstanten Aij. Die xi-Werte in der Tabelle müssen das Streckverhältnis 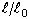angeben, und die yi-Werte müssen Werte für die technische Spannung 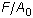sein. Spannungen werden für Druck negativ und für Zug positiv angegeben. Wenn diese Konvention nicht befolgt wird, kann die Konvergenz der Lösung fehlschlagen.
    • Äquibiaxiale Spannung: Daten für die Prognose der Materialkonstanten Aij. Die xi-Werte in der Tabelle müssen das Streckverhältnis 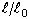angeben. Die yi-Werte müssen Werte für die technische Spannung 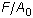sein. 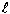ist die aktuelle Länge, F ist die aktuelle Kraft, 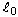ist die anfängliche Länge und 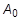ist der Querschnittsbereich. Im Fall von Druck einer kugelförmigen Membran wird die technische Spannung durch 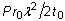ausgedrückt, wobei P der aktuelle Wert für den Druck und 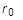bzw. 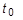der anfängliche Radius bzw. die anfängliche Stärke sind.
    • Einfache Scherung: Daten für die Prognose der Materialkonstanten Aij. Die xi-Werte in der Tabelle müssen Werte für die Schertangente 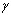sein, und die yi-Werte müssen Werte für die technische Spannung 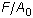sein.
    • Reine Scherung: Daten für die Prognose der Materialkonstanten Aij. Die xi- und yi-Werte in der Tabelle müssen Werte für das Streckverhältnis 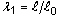und Werte für die Nennspannung 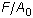sein. 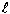ist die aktuelle Länge, F ist die aktuelle Kraft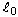, und und 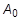sind die anfängliche Länge und der Querschnittsbereich in der Richtung 1.
    • Reiner volumetrischer Druck: Daten für die Prognose der Materialkonstanten Di. Die xi-Werte in der Tabelle müssen Werte für das Volumenverhältnis 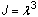sein, wobei 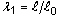das Streckverhältnis in alle drei Richtungen ist. Die yi-Werte müssen Werte für den Druck sein, der in der Komprimierung als positiv angenommen wird.