Für transiente Analysen werden die transienten Parameter mittels einer impliziten oder Rückwärtsdifferenzmethode diskretisiert. Mithilfe der Matrix-Algebra-Schreibung kann eine typische stationäre Transportgleichung (Impuls-, Energie-, Turbulenzvariablen, Skalar) wie folgt geschrieben werden:
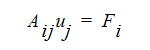
wobei Aij die diskretisierten Advektions- und Diffusionsparameter aus den zugrunde liegenden Gleichungen enthält, uj der Lösungsvektor ist bzw. die Werte der abhängigen Variablen (u, v, w, T, K,...) sind und Fi die Quellparameter enthält.
Die transienten Parameter der zugrunde liegenden Gleichungen nahmen folgende Form an:
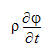
wobei 
die abhängige Variable (u, v, w, ...) darstellt. Dieser Ausdruck wird mit einer Rückwärtsdifferenz diskretisiert:
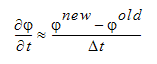
Dieser Ausdruck kann obiger Matrixgleichung hinzugefügt werden:
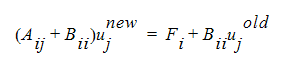
wobei Bii eine diagonale Matrix aus Ausdrücken wie folgenden ist:
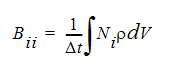
Diese diskretisierten transienten Gleichungen müssen iterativ bei jedem Zeitschritt gelöst werden, um alle neuen Variablen (variable Werte zur neuesten Zeit) zu bestimmen.