Die meisten Randbedingungen in Autodesk® CFD können über die Zeit veränderlich festgelegt werden. Dies ist hilfreich, um die Auswirkungen auf dem Gerät zu simulieren, wenn Strömungs-, Druck- oder Energiewerte sinken oder steigen.
Damit sich eine Randbedingung mit der Zeit verändert, öffnen Sie zunächst das Schnellbearbeitungs-Dialogfeld Randbedingungen. (Klicken Sie in der kontextabhängigen Gruppe "Randbedingungen" auf Bearbeiten):
- Ändern Sie im Dialogfeld "Randbedingung" die Zeit zu Transient.
- Wählen Sie die Methode Zeitkurve aus, und geben Sie die Parameter in das Popup-Dialogfeld ein. Es gibt sieben Methoden, damit sich die Lasten mit der Zeit verändern.
- Überprüfen Sie die Variation, indem Sie auf die Schaltfläche Plotten klicken. Dies ist hilfreich, um sicherzustellen, dass die Variation wie gewünscht funktioniert.
Konstant
Die konstante Variationsmethode hält den Wert während der gesamten Analyse konstant. Dies entspricht dem Zuweisen einer stationären Randbedingung.
Ein typischer Anwendungsbereich für "Konstant" wäre als Platzhalter für eine transiente Randbedingung zu einem späteren Zeitpunkt in der Analyse. Sie können zunächst einen konstanten Wert als transiente Bedingung zuweisen und diesen später zu einer anderen Variationsmethode ändern.
Stufenschritt
Die Stufenschritt-Funktion umfasst eine Funktion mit linearem Anstieg mit einer abgeflachten Stufenfunktion.
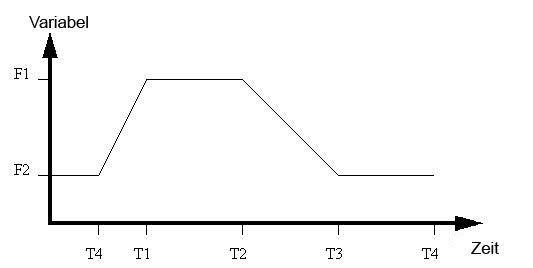
Die T-Werte sind die Zeiten, zu denen Wendepunkte auftreten.
Die F-Werte sind die Min- und Max-Werte der Variablen.
- Legen Sie die Funktion so fest, dass der maximale Wert (F1) erst bei Zeit T1 erscheint.
- Bei Zeit T2 beginnt der Wert zu sinken.
- Bei Zeit T3 erreicht die Funktion ihren Mindestwert (F2).
- Bei Zeit T4 beginnt der Wert zu steigen.
Periodisch
Der periodische Typ der Randbedingung ist exponentiell in der Zeit. Die Funktion lautet:
F(t) = A1 * e (B1*t + C1) + A2 * e(B2*t + C2)
.
Es ist nur ein Satz von Werten erforderlich: Geben Sie entweder A1, B1 und C1 ein ODER A2, B2 und C2.
Die Funktion kann mit der Zeit durch die Eingabe von negativen Werten für B1 oder B2 absinken.
Harmonisch
Die Funktion für die harmonische Variation lautet:
F(t) = A1 * cos(B1*t + C1) + A2 * sin(B2*t + C2)
Harmonisch variiert die Menge mit der Zeit als Funktion der Sinus- und Kosinus-Funktionen.
Es ist nur ein Satz von Werten erforderlich: Geben Sie entweder die Kosinuswerte (A1, B1 und C1) ein ODER die Sinuswerte (A2, B2 und C2).
Polynom und inverses Polynom
Eine Polynomfunktion erstellt eine Kurve zwischen den eingegebenen Koordinaten in Abhängigkeit ihrer Ordnung.
- Geben Sie die Wert- und Zeit-Daten in die Tabelle ein. (Zeit wird immer in Sekunden angegeben.)
- Geben Sie die Ordnung der Kurvenangleichung ein.
- Überprüfen Sie die Kurvenangleichung durch Klicken auf die Schaltfläche Plotten.
Potenzgesetz
Die Potenzfunktion hebt die Zeit mit der folgenden Funktion auf einen Exponenten an:
F(t) = A0 + A1*t(X)
- Geben Sie die Werte für die Koeffizienten A0 und A1 und den Exponenten X an.
Stückweise linear
Eine stückweise lineare Funktion verbindet die Datenpunkte mit linearen Segmenten und interpoliert dazwischen.
- Geben Sie die Daten für den Wert und die Zeit in die Tabelle ein. (Zeit wird immer in Sekunden angegeben.)
- Überprüfen Sie die Kurvenangleichung durch Klicken auf die Schaltfläche Plotten.
Vorgabemäßig wird eine stückweise lineare Funktion nur im festgelegten Zeitraum erstellt. Nach dem festgelegten Zeitraum wird der Wert der Bedingung für die Dauer der Analyse konstant gehalten. Um eine Funktion unendlich zu wiederholen, aktivieren Sie das Kontrollkästchen Vorgang wird wiederholt.
Verwandte Themen