Diese Seite beschreibt die Reibungsparameter für den allgemeinen Flächen-Flächen-Kontakt in nichtlinearen Simulationen, die mit dem programmeigenen Solver von Simulation Mechanical (SimMech-Solver) ausgeführt werden. Diese Parameter sind im Dialogfeld Kontaktoptionen auf der Registerkarte Reibung zu finden. Diese Registerkarte ist nur sichtbar, wenn Sie das Kontrollkästchen Reibung einbeziehen auf der Registerkarte Allgemein aktivieren.
Bei reibungslosem Kontakt sind die Matrizen der Elementsteifheit symmetrisch. Wenn Reibung beteiligt ist, wird die Matrix asymmetrisch. Die Verwendung eines asymmetrischen Solvers ist in Bezug auf den Rechenaufwand teurer als die Verwendung eines symmetrischen Solvers. Aufgrund der Effizienz erfordert MES die Symmetrie der Elementsteifheit, sodass der symmetrische Solver für Reibungskontakt verwendet werden kann.
Wenn Reibungskontakt in der Analyse berücksichtigt wird, wird der Lösungsvorgang durch den Gleitvorgang sehr anfällig. Wenn die Kontaktflächen beginnen zu gleiten, ist der Gleichgewichtszustand vor der Gleitbewegung nicht mehr zulässig. Der Gleichungslöser muss während des Lösungsvorgangs einen neuen Gleichgewichtszustand finden. Darüber hinaus ist aufgrund der Symmetrieannäherung eine unzureichende Konvergenz möglich. Jede der verfügbaren Reibungsgesetzoptionen versucht, die Instabilität auf unterschiedliche Weise zu steuern.
Wählen Sie das gewünschte Reibungsgesetz aus dem Dropdown-Menü oben in der Registerkarte Reibung aus. In Simulation Mechanical stehen für den nichtlinearen Fläche-Fläche-Kontakt drei Optionen zur Verfügung:
- Geänderte Coulomb-Reibung
- Coulomb mit viskose Reibung
- Geglättete Coulomb-Reibung
Jedes dieser Reibungsgesetze und die in diesem Zusammenhang angewendeten Parameter werden in den folgenden Unterabschnitten erörtert.
Geänderte Coulomb-Reibung
Dieses Reibungsgesetz verwendet den klassischen Reibungsalgorithmus: Coulomb-Reibung. Im grundlegenden Modell der Coulomb-Reibung können zwei Kontaktflächen der Scherspannung bis zu einer bestimmten Menge entgegenwirken, die anhand von Reibungskoeffizienten und normalem Kontaktdruck festgelegt wurde, bevor relative Gleitbewegungen auftreten. Das Modell der Coulomb-Reibung wird als τ = μP definiert, wobei μ der Reibungskoeffizient und P der normale Kontaktdruck ist. Sie müssen die folgenden drei Parameter definieren, wenn Sie das modifizierte Coulomb-Reibungsgesetz verwenden:
- Statischer Reibungskoeffizient (μs)
- Gleitreibungskoeffizient (μd)
- Tangentiales Steifigkeitsverhältnis
Sobald die Scherspannung μsP überschreitet, die aus der Eingabe Statischer Reibungskoeffizient resultiert, beginnen die beiden Flächen im besten Fall an zu gleiten. Darüber hinaus wird die Scherspannung zu μdP, wobei der Gleitreibungskoeffizient-Wert verwendet wird.
Die ideale Situation (keine Bewegung, bis die Scherspannung den statischen Wert überschreitet) ist numerisch schwierig zu erreichen, wie in Abbildung 1 beschrieben. Folglich wird ein Tangentiales Steifigkeitsverhältnis festgelegt, wenn dieses Reibungsgesetzt verwendet wird. Das tangentiale Steifigkeitsverhältnis ist das Verhältnis der tangentialen Kontaktsteifheit (Kt) zur Kontaktsteifheit in der Normalrichtung (K), das auf der Registerkarte Erweitert festgelegt wird. (Weitere Informationen finden Sie im Abschnitt Registerkarte Erweitert auf dieser Seite.) Eine größere tangentiale Steifigkeit führt zu einer besseren Genauigkeit, jedoch sind mehr Wiederholungen erforderlich. Eine geringere tangentiale Steifigkeit bietet bessere Konvergenz (kürzere Laufzeit) mit reduzierter Genauigkeit. Der empfohlene Wert liegt in einem Bereich von 0,01 bis 1. Wenn der statische Reibungskoeffizient größer wird, ist ein geringeres tangentiales Steifigkeitsverhältnis ratsam.
|
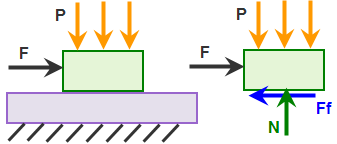
(a) Abbildung des Modells und freien Körpers für den oberen Block. Die angewendete Kraft F wird mit der Zeit erhöht, bis sie die Haftreibung überschreitet. |
|
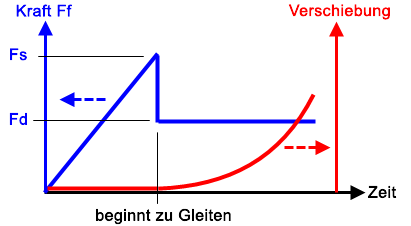
(b) Plot der Reibungskraft Ff vs. Zeit (blaue Kurve) und Verschiebung vs. Zeit (rote Kurve). Bis die Reibungskraft Ff die Grenze der Haftreibung erreicht (Fs = μs * N), gibt es keine Bewegung des Bauteils. Nachdem die Haftreibung überschritten wurde, fällt die Reibungskraft Ff von Fs auf Fd (= μd * N), und das Bauteil beginnt zu beschleunigen. |
|
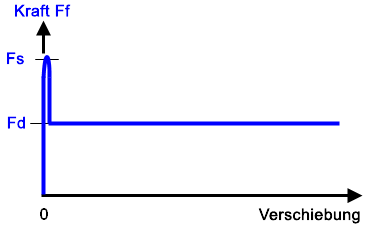
(c) Die Diagramme in Abbildung (b) werden kombiniert, um die Reibungskraft vs. Verschiebung zu zeigen. Im Idealfall gibt es keine Verschiebung, bis die Reibungskraft Fs erreicht, und die Gleitbewegung beginnt. Numerisch ist dies schwierig zu erreichen, da jede von Null verschiedene Verschiebung eine Reibungskraft von Fd beinhaltet. |
|
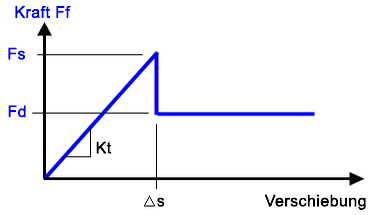
(d) Um die numerische Instabilität in Abbildung (c) zu vermeiden, kann das Bauteil etwas verschoben werden (Δs), während die Reibungskraft kleiner ist als die Haftreibungsgrenze (Fs). Die Bewegung wird durch die tangentiale Steifigkeit (Kt = Fs/Δs) gesteuert. Durch kleinere Kt-Werte kann das Bauteil weiter verschoben werden, bevor die Gleitbewegung einsetzt. Außerdem ist das Konvergieren einfacher, während höhere Kt-Werte (stärkere Neigung) geringere Verschiebungen ermöglichen, bevor die Gleitbewegung einsetzt. Sie führen außerdem zu erschwertem Konvergieren. Die tangentiale Steifigkeit wird anhand des tangentialen Steifigkeitsverhältnisses x Steifigkeit in der Normalrichtung berechnet. |
| Abbildung 1: Tangentiale Steifigkeit für modifizierte Coulomb-Reibung |
Coulomb mit viskose Reibung
Im Gegensatz zu dem geänderten Coulomb-Reibungsgesetz werden statische und dynamische Reibungskoeffizienten im Coulomb mit viskose Reibungsgesetz nicht berücksichtigt. Im modifizierten Coulomb-Reibungsgesetz ist eine relativ hohe Kraft erforderlich, um die statische Reibung zu überwinden und Bewegung zu starten. Sobald die Reibung beginnt, nimmt die Reibungskraft ab, da der Gleitreibungskoeffizient kleiner als der statische Koeffizient ist. Daher tritt eine Kraftdiskontinuität aufgrund der abrupten Änderung in der Reibungskraft auf. Beim Reibungsgesetz Coulomb mit viskoser Reibung gibt es keine Reibungskraftdiskontinuität, wenn das Gleiten beginnt. Stattdessen wird die Reibungskraft beim Erhöhen der Geschwindigkeit allmählich erhöht.
Für die Option Coulomb mit viskose Reibung müssen Sie zwei Parameter definieren:
- Gleitreibungskoeffizient (Fd): Dies wird auch als dynamischer Reibungskoeffizient bezeichnet. Es ist das Verhältnis der tangentialen Kraft, die notwendig ist, um die relative Bewegung und die normale Kraft zwischen den sich berührenden Bauteilen beizubehalten. Beispiel: Wenn 15N tangentialer Kraft erforderlich sind, um einen Block entlang eines angrenzenden Bauteils beizubehalten, und die normale Kontaktkraft dazwischen 100N beträgt, lautet der Gleitreibungskoeffizient 15N / 100N = 0,15. In Anbetracht dieses Reibungsgesetzes sollten Sie die Gleitgeschwindigkeit für den Gleitreibungskoeffizienten relativ gering halten.
- Viskose Reibungskoeffizient (νs): Dies ist die Neigung der Reibungskraft im Vergleich zur Schiebegeschwindigkeitskurve. Für alle viskose Effekte gilt, dass die Kraft, die zur Überwindung der viskosen Effekte notwendig ist, proportional zur Geschwindigkeit ist.
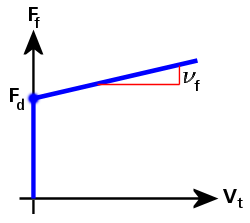
Abbildung 2: Reibungskraft im Vergleich zur Gleitgeschwindigkeit (Coulomb mit viskoser Reibung)
In Abbildung 2 wird die Kurve für die Reibungskraft (Ff) wie folgt definiert:
Ff = Fd + νf · Vt
Dabei gilt:
Fd ist die dynamische (gleitende) Reibungskraft,
νf ist der viskose Reibungskoeffizient und
Vt ist die tangentiale (gleitende) Geschwindigkeit zwischen den beiden Bauteilen.
Wenn νf = 0 ist, ist Ff = Fd
Geglättete Coulomb-Reibung
Wie die Coulomb mit viskose Reibung , berücksichtigt auch die Geglättete Coulomb-Reibung nur den Gleitreibungskoeffizienten. Auf diese Weise scheidet die Diskontinuität der Reibungskraft zwischen den statischen und gleitenden Bedingungen bei Verwendung des Ändern der Coulomb-Reibung-Gesetzes aus. Der Übergang zwischen statischen und gleitenden Bedingungen wird zudem durch die Integration eines gleichmäßigen Übergangsfaktors (Φ) stabilisiert.
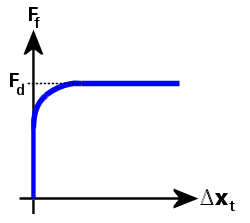
Abbildung 3: Reibungskraft im Vergleich zur tangentialen relativen Verschiebung (geglättete Coulomb-Reibung)
In Abbildung 3 wird die Kurve für die Reibungskraft (Ff) wie folgt definiert:
Ff = Fd · Φ, und
Φ = tanh(3 · Δxt / δ)
Dabei gilt:
Fd ist die dynamische (gleitende) Reibungskraft.
Φ ist ein Übergangsfaktor, der die Reibungskraft gleichmäßig bis null gleiten lässt, wenn die tangentiale relative Verschiebung null erreicht. In ähnlicher Weise gleitet die Reibungskraft gleichmäßig bis zur dynamischen Reibungskraft, wenn sich die tangentiale relative Verschiebung erhöht.
Δxt ist die tangentiale relative Verschiebung und
δ ist eine Toleranz, die basierend auf der Kontaktsteifheit und dynamischen Reibungskraft berechnet wird.