Capture the nonlinear behavior of fibers under large axial strains.
It is generally known that the modulus of fibers can exhibit nonlinear elasticity when subject to large axial strains. When the axial fiber strain is tensile, fibers tends to stiffen and when the axial fiber strain is compressive, fibers tends to soften. Both of these behaviors are captured via the *NONLINEAR FIBER keyword. This keyword must be preceded by the *MATERIAL keyword so that the material of interest is properly identified:
*NONLINEAR FIBER, ETAC=Compressive Knockdown Factor GAMMA_1T, GAMMA_1C
ETAC and GAMMA_1C are mutually exclusive options.
For tensile loading, the following equation is used to approximate the nonlinear elastic stiffening of the fiber (and thus the composite):
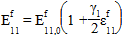
Where:
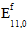is the original fiber modulus
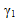is the nonlinear fiber parameter (GAMMA_1T)
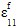is the axial fiber strain (assumed to be equal to the axial composite strain)
For compressive loading, a simple relationship is used to approximate the modulus softening if ETAC is specified:
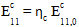
Where:
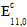is the original composite modulus
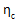is the composite modulus knockdown factor (ETAC)
For compressive loading with GAMMA_1C specified, the following equation is used to approximate the nonlinear elastic softening of the fiber (and thus the composite):
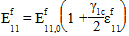
Where:
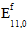is the original fiber modulus
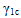is the nonlinear fiber parameter for compression (GAMMA_1C)
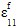is the axial fiber strain (assumed to be equal to the axial composite strain)
The fiber modulus is considered nonlinear until fiber failure occurs. Once fiber failure occurs, the composite stiffnesses will remain fixed because their influence is negligible and continuing to update the properties would be an inefficient use of computational resources.
*MATERIAL, NAME=IM7_8552 *NONLINEAR FIBER, ETAC=0.75 21.0
For further information regarding the fiber nonlinearity features, refer to the Theory Manual.
