Input Parameters for Defining Cohesive Constitutive Relations

Review the constants used to define the cohesive material constitutive relations.

Helius PFA's cohesive UMAT is compatible with any of the 2-D or 3-D cohesive elements provided by Abaqus/Standard (e.g., COH2D4, COH3D8, etc.). The cohesive constitutive relations are formulated as traction/separation laws that define the transverse normal traction and transverse shear traction of the cohesive material in terms of the relative displacements between the upper and lower surfaces of the cohesive element. These traction/separation laws for the cohesive material are defined via a small number of user-specified constants described below.

Note: It should be emphasized that the constitutive laws currently implemented in the Helius PFA cohesive UMAT represent a subset of the cohesive constitutive relations currently provided by Abaqus/Standard. Consequently, the Abaqus/Standard documentation can also be consulted as an additional reference for the constitutive relations of Helius PFA's cohesive UMAT. The main difference is that the constitutive relations of Helius PFA's cohesive UMAT have been treated with convergence enhancing methodology.

Stiffness (K_nn, K_ss, K_tt)

The stiffness of the cohesive material is defined via three constants (K_nn, K_ss, K_tt) which are input as material moduli of the cohesive material (units of force/area). K_nn is the original un-damaged transverse normal modulus of the cohesive material, while K_ss and K_tt are the original un-damaged transverse shear moduli of the cohesive material. Within the cohesive UMAT, these material moduli (K_nn, K_ss, K_tt) are scaled via the thickness of the cohesive element to express stiffness in units appropriate for relating traction to relative displacements of the upper and lower surfaces of the cohesive element.

Initiation Strengths (S_n, S_s, S_t)

Prediction of damage initiation in the cohesive material is traction-based and depends entirely on the transverse normal traction (t _n ) and the transverse shear tractions (t _s and t _t ) borne by the cohesive material. For a pure transverse normal loading of the cohesive material, S_n is the normal traction (t _n ) at which damage initiation occurs. For pure transverse shear loading of the cohesive material, S_s and S_t are the shear tractions (t _s and t _t ) at which damage initiation occurs.

Helius PFA provides two different traction-based criteria to signal delamination initiation (or damage initiation) of the cohesive material, namely, the Max Stress Criterion and the Quadratic Stress Criterion (described later).

Dissipation Energy of Delamination

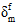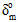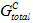( - ), (), or (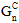, , 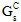, 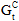α)

There are three different methods for specifying the amount of energy dissipated by the cohesive material during the delamination process. These methods are referred to as the total displacement model (where you specify 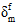- 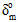), the total energy model (where you specify 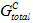), and the mixed mode power law (where you specify 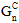, , 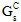, 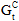α).