Properties

Determine the effective engineering properties of a laminate.

The effective engineering properties of a laminate are computed by selecting the Properties tab from the Laminate Properties window. Once a laminate is defined in the Laminate tab, click the Calculate button to compute the laminate engineering properties. Helius Composite computes the laminate's 2-D and 3-D properties and displays the results in the 2-D and 3-D display windows of the Properties tab (see image below).

Note: This function is also available by right clicking on an existing laminate in the file tree and selecting Laminate Engineering Props.

After the laminate engineering properties are displayed, three different options that can be invoked within the Properties tab.

1. Plot Moduli - This button displays a bar graph of the extensional and bending moduli as well as the shear modulus. This is particularly handy for visualizing the magnitude of the differences in the moduli.
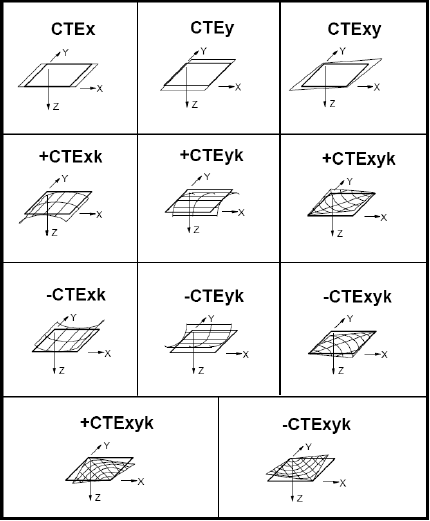
2. Plot CTE - This button creates a bar graph that displays all six laminate coefficients of thermal expansion: three extensional coefficients (CTEx, CTEy, and CTExy) and three curvature coefficients (CTExk, CTEyk, and CTExyk). This is particularly handy for visualizing the difference in magnitude between CTE's. The curvature CTE's are of particular interest because they show the magnitude of the un-symmetric or unbalanced nature of the laminate. Whenever the CTE plot shows curvature coefficients of magnitude greater than or equatl to the extensional coefficients, the laminate will show some degree of warping.
3. Add to LAMINA Properties - This button automatically creates a new lamina material whose properties are equivalent to the effective 3-D properties of the current laminate. The name of the new lamina material will be the same as the name of the current laminate. The new lamina material will be visible under the Laminas branch of the Material Data File tree.

The following list briefly describes some of the 2-D and 3-D laminate properties computed by the Laminate Engineering Props feature.

Laminate Extension and Shearing Moduli:

EX (psi)

Effective Young's modulus of the laminate in the global X-direction

EY (psi)

Effective Young's modulus of the laminate in the global Y-direction

EZ (psi)

Effective Young's modulus of the laminate in the global Z-direction

Gxy (psi)

Effective shear modulus of the laminate in the global XY-plane

Gxz (psi)

Effective shear modulus of the laminate in the global XZ-plane

Gyz (psi)

Effective shear modulus of the laminate in the global YZ-plane

Laminate Poisson Ratios:

NUxy

Poisson ratio interpreted as the free contraction of the laminate mid-plane in the global Y direction in response to an imposed extension of the laminate mid-plane in the global X direction.

NUyx

Poisson ratio interpreted as the free contraction of the laminate mid-plane in the global X direction in response to an imposed extension of the laminate mid-plane in the global Y direction.

NUxz

Poisson ratio interpreted as the free contraction of the laminate mid-plane in the global Z direction in response to an imposed extension of the laminate mid-plane in the global X direction.

NUzx

Poisson ratio interpreted as the free contraction of the laminate mid-plane in the global X direction in response to an imposed extension of the laminate mid-plane in the global Z direction.

NUyz

Poisson ratio interpreted as the free contraction of the laminate mid-plane in the global Z direction in response to an imposed extension of the laminate mid-plane in the global Y direction.

NUzy

Poisson ratio interpreted as the free contraction of the laminate mid-plane in the global Y direction in response to an imposed extension of the laminate mid-plane in the global Z direction.

Note: The following relationship exists between the corresponding pairs of Poisson ratios:

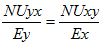
Laminate Flexural Properties:

Exb (psi)

Laminate bending modulus in global YZ-plane.

Eyb (psi)

Laminate bending modulus in global XZ-plane.

Gxyb (psi)

Laminate twisting modulus associated with twisting deformation that produces displacement in the global Z-direction.

Thermal Deformation Coefficients:

CTEx (in/in/F)

Thermal expansion coefficient of the laminate in the global X-direction. This coefficient governs the free expansion or contraction of the laminate mid-plane in the global X-direction due to a uniform temperature change.

CTEy (in/in/F)

Thermal expansion coefficient in the global Y-direction. This coefficient governs the free expansion or contraction of the laminate mid-plane in the global Y-direction due to a uniform temperature change.

CTExy (in/in/F)

Thermal shear coefficient in the global XY-plane. This coefficient governs the free in-plane shear deformation of the laminate mid-plane in the global XY-plane due to a uniform temperature change.

CTExk (in/in/F)

Thermal curvature coefficient in the global YZ-plane. This coefficient governs the free bending of the laminate mid-plane in the global YZ-plane due to a uniform temperature change.

CTEyk (in/in/F)

Thermal curvature coefficient in the global XY-plane. This coefficient governs the free bending of the laminate mid-plane in the global XZ-plane due to a uniform temperature change.

CTExyk (in/in/F)

Thermal twisting coefficient associated with displacements in the global Z-direction. This coefficient governs the free out-of-plane twisting of the laminate mid-plane due to a uniform temperature change.

Note: The image below shows the free thermal deformation associated with each of the laminate coefficients of thermal expansion and curvature.

Moisture Expansion Coefficients:

The coefficients of moisture expansion (CME) are completely analogous to the thermal expansion coefficients described previously. The only difference is that the magnitude of deformation is dependent on the uniform % moisture change instead of being dependent on the uniform temperature change.