Calculate the laminate stiffness matrix.
In Classical Laminate Theory, the [A], [B], and [D] matrices collectively form the laminate stiffness matrix. The laminate stiffness matrix is used to express laminate resultant forces per unit width {N} and laminate resultant moments per unit width {M} in terms of laminate mid-plane strains {e 0 } and laminate mid-plane curvatures {k}. This is shown in Eq. 5.1.
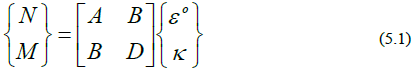
In Classical Laminate Theory, the [A'], [B'], and [D'] matrices collectively form the laminate compliance matrix. The laminate compliance matrix is used to express laminate mid-plane strains {e o } and laminate mid-plane curvatures {k} in terms of laminate resultant forces per unit width {N} and laminate resultant moments per unit width {M}. This is shown in Eq. 5.2.
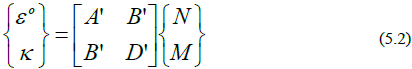
In Helius Composite, the laminate compliance matrix is referred to as the [ABD] inverse matrix. The individual 3x3 matrices [A'], [B'], and [D'] of Eq. 5.2 are referred to as the [A] inverse, [B] inverse, and [D] inverse matrices.
Once a laminate has been defined in the Laminate tab, select the ABD Matrices tab to compute the [A], [B], and [D] matrices for the laminate. Click the ABD Inverse Matrices tab to compute the [A'], [B'], and [D'] matrices for the laminate. In either case, click the Calculate button to compute the matrices and display the results. The image below shows the ABD Matrices tab and ABD Inverse Matrices tab after you have clicked the Calculate button. After the matrices are computed and displayed, click Export to write the results to a *.csv file compatible with Microsoft Excel.

