General Calculation Formulas
Outside spring diameter
D 1 = D + d [in]
where:
|
D |
mean spring diameter [in] |
|
|
d |
wire diameter [in] |
Inside spring diameter
D 2 = D - d [in]
where:
|
D |
mean spring diameter [in] |
|
|
d |
wire diameter [in] |
Torque for the preloaded spring
![]()
where:
|
F 1 |
working force for the preloaded spring [lb] |
|
|
R 1 |
arm of working force [in] |
Torque for the fully loaded spring
![]()
where:
|
F 8 |
working force (for the fully loaded spring) [lb] |
|
|
R 1 |
arm of working force [in] |
Spring index
i = D/d [-]
where:
|
D |
mean spring diameter [in] |
|
|
d |
wire diameter [in] |
Angle of working stroke
ϕ h = ϕ 8 - ϕ 1 [°]
where:
|
ϕ 8 |
angle deflection of working arm for the fully loaded spring [°] |
|
|
ϕ 1 |
angle deflection of working arm for the preloaded state [°] |
Minimum angle deflection of working arm
![]()
where:
|
M 1 |
torque for the preloaded spring [lb ft] |
|
|
k |
torsional spring rate [lb ft/°] |
|
|
ϕ h |
angle of working stroke [°] |
|
|
M 8 |
torque for the fully loaded spring [lb ft] |
Maximum angle deflection of working arm
![]()
where:
|
M 1 |
torque for the preloaded spring [lb ft] |
|
|
k |
torsional spring rate [lb ft/°] |
|
|
ϕ h |
angle of working stroke [°] |
|
|
M 8 |
torque for the fully loaded spring [lb ft] |
Stress concentration factor
![]()
where:
|
i |
Spring index [-] |
|
|
i = D/d [-] |
for calculation of bending stress in active coils |
|
|
|
for calculation of stress in the arm bending |
|
|
r |
bending radius at the arm (internal) [in] |
|
|
d |
wire diameter [in] |
Spring material stress, in general
![]()
where:
|
M |
torque for the spring, in general [Nm] |
|
|
K f |
stress concentration factor [-] |
|
|
d |
wire diameter [in] |
Number of spring active coils
![]()
where:
| ϕ |
angle deflection of working arm, in general [°] |
|
|
E |
modulus of elasticity [psi] |
|
|
d |
wire diameter [in] |
|
|
M |
torque for the spring, in general [lb ft] |
|
|
R 1 |
arm of working force [in] |
|
|
R 2 |
arm of support force [in] |
|
|
D |
mean spring diameter [in] |
Spring Design Calculation
During the design of a spring, wire diameter, number of coils, and the bending diameter of bend hook arm are designed to comply with the specific load, material, and assembly dimensions. Design springs to suit the recommended wire diameters. For springs with a clearance between coils, the t pitch between spring threads in free state must fall within the range of 0.3 D ≤ t ≤ 0.5 D [in].
The spring design is based on the (σ 8 ≤ u s sA) and (σ 8r ≤ u s σ A ) strength condition and the recommended ranges of some spring geometric dimensions.
L Z ≤ 10 D and L Z ≤ 31.5 in and 4 ≤ D/d ≤ X and n≥ 1.5 and 1.2 d ≤ t < D and r ≥ d.
where:
- Spring with close-wound coils X = 16
- Spring with loose-wound coils X = 10
Spring dimensions conform to the practicable geometric solution in accordance with the specified shape and length of arms. If set in the specification, the dimensions must comply with the limit dimensions of mounting, which are the maximum allowable housing diameter and length or the maximum allowable rod diameter).
Specified maximum load, material, and spring assembly dimensions
First the input values for the calculation are checked and calculated.
Then the minimum load is calculated for specified maximum load and assembly dimensions.
![]()
where:
|
M 1 |
torque for the preloaded spring [lb ft] |
|
|
M 8 |
torque for the fully loaded spring [lb ft] |
|
|
ϕ 1 |
angle deflection of working arm for the preloaded state [°] |
|
|
ϕ 8 |
angle deflection of working arm for the fully loaded spring [°] |
The wire diameter and number of coils are designed so that after calculating the spring diameter, the strength, and geometric conditions are fulfilled. If the spring diameter value is limited in the specification, then the spring design must conform. If not so, the limits of spring diameter are determined by the geometric conditions for minimum and maximum allowable wire diameter.
For springs with hook arms, suitable radii of arm bendings are designed.
All spring wire diameters with the specified strength and geometric conditions are calculated, starting with the smallest wire diameter, and working to the largest. Then the compliance with all required conditions for suitable coil numbers is tested. If all conditions are met, the design is finished with the selected values, regardless of possibly remaining compliant spring wire diameters, and a spring is designed with the smallest possible wire diameters, the lowest number of coils, and lowest spring diameters.
Specified load, material, and working deflection angle
First, the input values for the calculation are checked.
For specified load and working deflection angle, working arm angle deflections are calculated next.
Minimum deflection of working arm
![]()
Maximum deflection of working arm
![]()
where:
|
M 1 |
torque for the preloaded spring [lb ft] |
|
|
M 8 |
torque for the fully loaded spring [lb ft] |
|
|
ϕ 1 |
angle deflection of working arm for the preloaded state [°] |
|
|
ϕ 8 |
angle deflection of working arm for the fully loaded spring [°] |
|
|
ϕ h |
angle of working stroke [°] |
Next, the wire diameter and number of coils are designed so that after calculating the spring diameter, the strength and geometric conditions are fulfilled. If the spring diameter value is limited in the specification, then the spring design must conform to that condition. Otherwise, the limits of spring diameter are determined by the geometric conditions for minimum and maximum allowable wire diameter.
For springs with the hook arms, suitable radii of arm bendings are designed.
All spring wire diameters with the specified strength and geometric conditions are considered, starting from the smallest wire diameters, and working to the largest. Next, the compliance with required conditions for suitable coil numbers is tested. If all conditions are met, the design is finished with the selected values, regardless of possibly remaining compliant spring wire diameters, and the spring is designed with the smallest possible wire diameters, the lowest number of coils, and lowest spring diameters.
Specified maximum load, material, and spring diameter
First the input values for the calculation are checked.
Next, the wire diameter, number of coils and assembly dimensions are designed to meet the strength and geometric conditions. If the working deflection angle value is limited in the specification, then the spring design must conform to this condition. If not so, the limits of assembly dimensions are determined by the geometric conditions for specified spring diameter and minimum or maximum allowable wire diameter.
For springs with the hook arms, suitable radii of arm bending are computed.
All spring wire diameters with the specified strength and geometric conditions are considered, and respective designs with increasing wire diameters from the smallest to the largest are calculated. Next, the compliance with all required conditions for coil numbers is tested. If all conditions are met, the design is finished with the selected values, regardless of possibly remaining compliant spring wire diameters, and the spring is designed with the smallest possible wire diameters, the lowest number of coils, and lowest spring diameters.
Specified maximum load, material, spring diameter, and working deflection angle
First the input values for the calculation are checked.
Next, the wire diameter, number of coils, and angle deflections of working arm are optimized to meet the strength and geometric conditions. The program seeks a minimum of maximum angle deflection of working arm ϕ 8 taking into account the requirement of minimum angle deflection of working arm ϕ 1 equaling about 2°.
For springs with hook arms, suitable radii of arm bending are computed.
Finally, for specified maximum load and designed angle deflections of working arm, the minimum spring load is calculated.
![]()
where:
|
M 1 |
torque for the preloaded spring [lb ft] |
|
|
M 8 |
torque for the fully loaded spring [lb ft] |
|
|
ϕ 1 |
angle deflection of working arm for the preloaded state [°] |
|
|
ϕ 8 |
angle deflection of working arm for the fully loaded spring [°] |
Spring Check Calculation
Calculates corresponding values of assembly dimensions for the specified load, material, and spring dimensions. First the input data are checked and calculated, then the assembly dimensions are calculated using the following formulas.
Minimum angle deflection of working arm
![]()
where:
|
M 1 |
torque for the preloaded spring [lb ft] |
|
|
D |
mean spring diameter [in] |
|
|
n |
number of active coils [-] |
|
|
R 1 |
arm of working force [in] |
|
|
R 2 |
arm of support force [in] |
|
|
E |
modulus of elasticity [psi] |
|
|
d |
wire diameter [in] |
Maximum angle deflection of working arm
![]()
where:
|
M 1 |
torque for the preloaded spring [lb ft] |
|
|
D |
mean spring diameter [in] |
|
|
n |
number of active coils [-] |
|
|
R 1 |
arm of working force [in] |
|
|
R 2 |
arm of support force [in] |
|
|
E |
modulus of elasticity [psi] |
|
|
d |
wire diameter [in] |
Angle of working stroke
ϕ h = ϕ 8 - ϕ 1 [°]
where:
|
M 8 |
torque for the fully loaded spring [lb ft] |
|
|
ϕ 8 |
angle deflection of working arm for the fully loaded spring [°] |
Calculation of Working Forces
Corresponding forces produced by springs in their working states are calculated for the specified material, assembly dimensions, and spring dimensions. The input data is checked and calculated, and then the working forces are calculated using the following formulas.
Minimum working load
![]()
![]()
where:
|
M 1 |
torque for the preloaded spring [lb ft] |
|
|
ϕ 1 |
angle deflection of working arm for the preloaded state [°] |
|
|
D |
mean spring diameter [in] |
|
|
n |
number of active coils [-] |
|
|
R 1 |
arm of working force [in] |
|
|
R 2 |
arm of support force [in] |
|
|
E |
modulus of elasticity [psi] |
|
|
d |
wire diameter [in] |
Maximum working load
![]()
![]()
where:
|
M 8 |
torque for the fully loaded spring [Nm] |
|
|
ϕ 8 |
angle deflection of working arm for the fully loaded spring [°] |
|
|
D |
mean spring diameter [in] |
|
|
n |
number of active coils [-] |
|
|
R 1 |
arm of working force [in] |
|
|
R 2 |
arm of support force [in] |
|
|
E |
modulus of elasticity [psi] |
|
|
d |
wire diameter [in] |
Calculation of spring output parameters
Common for all types of spring calculation, and calculated in the following order.
Torsional spring rate
![]()
Space between coils for the loose spring
a = t - d [mm]
Length of spring coiled part for the loose spring
|
for close-wound spring |
|
|
L 0 = 1.05 (n + 1) d [in] |
|
|
for loose-wound spring |
|
|
L 0 = t n + d [in] |
|
Bending stress of the spring material in active coils for minimum working load
![]()
where the stress concentration factor K f is calculated for i = D/d
Bending stress of the spring material at the arm bend for minimum working load
![]()
where the stress concentration factor K f is calculated for i = 2r/d + 1
Bending stress of the spring material in active coils for the fully loaded state
![]()
where the stress concentration factor K f is calculated for i = D/d
Bending stress of the spring material at the arm bend for the fully loaded state
![]()
where the stress concentration factor K f is calculated for i = 2r/d + 1
Length of coiled spring part in the fully loaded state for the close-wound spring and the load coils the spring
![]()
Spring outside diameter in the fully loaded state and the load coils the spring
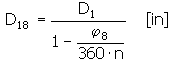
Spring inside diameter in the fully loaded state and the load coils the spring
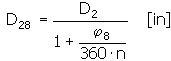
Limit test angle deflection of working arm
![]()
Spring deformation energy
![]()
Wire length
|
l = 3.2 D n + l R [in] |
||||
|
where the l R is an arm length, while: |
||||
|
where the l R is an arm length, while: |
||||
|
length of straight torsion arm |
||||
|
|
||||
|
length of hook arm |
||||
|
|
||||
Spring mass
![]()
Check of spring load
(σ 8 ≤ u s σ A ) and (σ 8r ≤ u s σ A )
Meaning of used variables:
|
a |
space between active coils in the free state [in] |
|
d |
wire diameter [in] |
|
D |
mean spring diameter [in] |
|
D 1 |
spring outside diameter [in] |
|
D 2 |
spring inside diameter [in] |
|
E |
modulus of elasticity [psi] |
|
F |
working force exerted by the spring (the force exerted on the R 1 arm of the working force), in general [lb] |
|
i |
spring index [-] |
|
K F |
stress concentration factor [-] |
|
kϕ |
torsional spring rate [lb ft/°] |
|
r 1 |
bending radius at the working arm [in] |
|
r 2 |
bending radius at the support arm [in] |
|
R 1 |
arm of working force [in] |
|
R 2 1 |
arm of support force [in] |
|
l |
wire length [in] |
|
L 0 |
length of coiled part in the loose state, in general [in] |
|
m |
spring mass [lb] |
|
M |
torque for the spring, in general [lb ft] |
|
n |
number of active coils [-] |
|
t |
pitch between coils in the loose state [in] |
|
u s |
|
| ρ |
density of spring material [lb/ft3] |
| ϕ |
angle deflection of working arm, in general [°] |
| σ |
bending stress of spring material, in general [psi] |
|
σ A |
allowable bending stress of spring material [psi] |
|
M 1 |
torque for the preloaded spring [lb ft] |
|
M 8 |
torque for the fully loaded spring [lb ft] |
|
ϕ 8 |
angle deflection of working arm for the fully loaded spring [°] |
|
ϕ 1 |
angle deflection of working arm for the preloaded state [°] |
|
ϕ 8 |
angle deflection of working arm for the fully loaded spring [°] |
|
ϕ h |
angle deflection of working arm for the fully loaded spring [°] |