この項は、数学におけるこの分野を復習するための簡単な解説です。三角関数に関する十分な知識があれば、省略して次に進んでください。このトピックの内容が難しい場合は、より基本的な参考書をお読みください。
三角関数は主に次の項目のモデリングや記述に使用します。
- 三角形の内角の関係(つまり名前)
- 円を中心とした回転。 極座標による位置も含む
- 循環的、または定期的値音波など
単位円を中心に回転する角度から 3 つの基本三角関数が導き出されます。
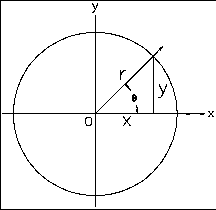
単位円を基本とする三角関数
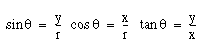
正接関数は x = 0 の場合は、定義できません。正接を定義するもう 1 つの方法は次のようになります。
XYR によって三角形の右角度が決まるため、サインとコサインの関係は次のようになります。
基本三角関数のグラフは、各関数の循環特性を表しています。
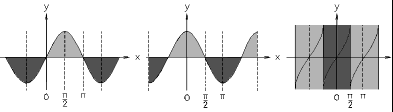
基本三角関数のグラフ
正弦関数と余弦関数からは同じ値が導かれますが、X 軸方向の位相が/2、πつまり 90 度ずれています。
三角関数の逆関数はアーク関数です。逆関数は、–π/2 ≤ X ≤ π/2 の範囲の x の値にのみ適用されます。これらの関数のグラフは、基本三角関数のグラフの左右が逆になったような形をしています。
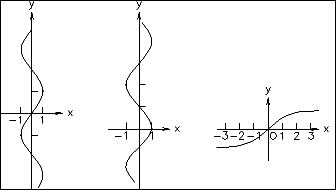
基本アーク関数のグラフ
双カーブ関数では、循環計測値の代わりに指数定数 e がベースになります。ただし、働きは三角関数に似ており、三角関数のために取りあげたものです。基本双曲線関数は、次のとおりです。
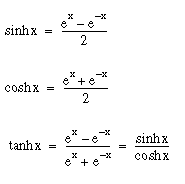
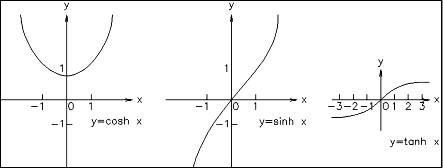
基本双曲線関数のグラフ