3D フロー結果は、次の考慮事項に基づいています。
金型キャビティ内での流動ーをシミュレーションするため、運動量、質量、およびエネルギーの保存方程式を運動量、エネルギー方程式は、有限要素に離散化されます。
これは、次の方程式によって定義されます。
流体の質量保存
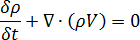
説明
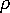 は樹脂密度
は樹脂密度 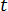 は時間
は時間 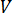 は速度ベクトル
は速度ベクトル
運動量保存
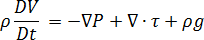
説明
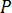 は圧力
は圧力  は粘性応力テンソル
は粘性応力テンソル 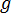 は重力加速度度ベクトル
は重力加速度度ベクトル
エネルギー保存
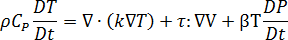
説明
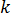 は樹脂熱伝導率
は樹脂熱伝導率 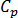 は特定の樹脂の比熱容量
は特定の樹脂の比熱容量 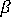 は、次のように定義される樹脂膨張
は、次のように定義される樹脂膨張
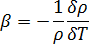
圧力-速度(運動量よび質量保存)解析の場合。
- 方程式は、標準の有限要素法によって解かれます。これには、すべての処理段階の材料の圧縮性が含まれます。
- ビームと四面体要素は同時に解かれます。
- 各ビーム要素のシャドウ内のすべての四面体ノードが同じ圧力に関連付けられます。
- ビーム要素では、1D フローが想定され、Hele-Shaw 近似が使用されます。
- 四面体要素では、フル ストローク解析が実行されます(または、慣性オプションを選択した場合は Navier-Stokes)です。
温度(エネルギー保存)解析の場合
- 方程式は、標準の有限要素法によって解かれます。
- ビーム要素と四面体要素の両方で、せん断発熱、熱対流、伝導、および圧縮加熱の項を含めます。
- ビーム要素では、ビームの長さに沿ったわずかな伝導の近似値を出します。ビーム要素の熱対流では、各ビーム ラミネート内でアップウィンドします。
- 温度方程式を計算する際、精度向上のため、タイム ステップを多くの短いサブステップに分割します。
各タイム ステップでは、収束するまで、温度方程式および圧力-速度方程式の間を反復します。