이 섹션에서는 다양한 편경사 접속 설치 방법에 사용할 수 있는 XML 형식의 예를 보여 줍니다.
표준 접속 설치 방법 예
다음 예에서는 AASHTO 표준 방법을 사용하여 분할되지 않은 크라운이 있는 도로에 대한 변환 측점을 계산하는 데 사용할 수 있는 XML 형식을 보여 줍니다.
<SuperelevationAttainmentMethod name="AASHTO 2001 - Crowned Roadway">
<AttainmentStyle style="Standard"/>
<TransitionFormula type="LCtoFS" formula="{t}"/>
<TransitionFormula type="LCtoBC" formula ="{p}*{t}"/>
<TransitionFormula type="NCtoLC" formula ="{t}*{c}/{e}"/>
<TransitionFormula type="LCtoRC" formula ="{t}*{c}/{e}"/>
<TransitionFormula type="NStoNC" formula ="{t}*({s}-{c})/{e}">
<SuperelevationAttainmentMethod>
이 예에서는 표준 역방향 크라운 편경사 접속 설치 방법을 사용하고 이름이 "AASHTO 2001 - 크라운이 있는 도로"인 접속 설치 방법을 정의합니다. 이 예는 길어깨 횡단경사변경부를 제거하는 데 필요한 변환 거리 계산을 포함합니다(유형="NStoNC").
평면형 변환 접속 방법 예
이 예에서는 분할되지 않은 평면형 도로를 보여줍니다. 이 도로에는 크라운이 없으므로 역방향 크라운 제거도 없습니다.
평면형 접속 설치 방법에는 표준횡단 경사와 방향이 반대인 원곡선과 표준횡단 경사와 동일한 방향인 원곡선에 대한 두 가지 공식이 필요합니다. 다음 그림은 한쪽으로 기울어지지 않는 도로가 왼쪽에서 오른쪽으로 아래로 기울어져 있기 때문에 왼쪽 원곡선에 오른쪽 원곡선보다 긴 변환이 필요한 일반 경사 편경사를 보여 줍니다.
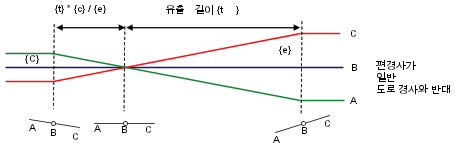
다음 예에서, 연속 횡단은 일반 크라운으로부터 최대 편경사까지의 거리 유출 길이 {t}(변환 길이 테이블에서 파생됨)에서, 유출 길이를 곱한 일반 도로 경사 {c}를 최대 편경사 설치율 {e}로 나눈 값을 뺀 값을 정의합니다. 두 번째 공식에서는 일반 크라운에서 원곡선 시작까지의 거리를 {c}를 {e}로 나눈 값을 변수 {p}에서 뺀 결과를 {t}와 곱한 값으로 정의합니다.
반대 횡단은 전체 변환 거리(유출 길이 {t})를 정의합니다. 원곡선 시작까지의 거리는 {t}를 변수 {p}와 곱한 값이며, 일반 크라운과 평 크라운 측점 간의 거리는 {t}*{c}/{e}입니다.
<SuperelevationAttainmentMethod name="Undivided Planar Roadway">
<TransitionStyle style="Planar"/>
<Continuing>
<TransitionFormula type="NCtoFS" formula="{t}-{t}*{c}/{e}"/>
<TransitionFormula type="NCtoBC" formula="{t}*({p}-{c}/{e})"/>
</Continuing>
<Opposing>
<TransitionFormula type="LCtoFS" formula="{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{t}"/>
<TransitionFormula type="NCtoLC" formula="{t}*{c}/{e}"/>
</Opposing>
<SuperelevationAttainmentMethod>
도로 폭 및 접속설치율에 의해 정의된 변환
모든 조직이 변환 길이를 직접 제공하는 테이블을 사용하지는 않습니다. 다음 테이블은 최대 편경사 설치율과 ![]() 을 설계 속도와 원곡선 반지름의 함수로 정의합니다. 이 경우
을 설계 속도와 원곡선 반지름의 함수로 정의합니다. 이 경우 ![]() 값은 도로의 일반 폭을 기반으로 변환 길이를 파생시키는 데 사용됩니다. 변환 길이 테이블은 실제 변환 길이 대신
값은 도로의 일반 폭을 기반으로 변환 길이를 파생시키는 데 사용됩니다. 변환 길이 테이블은 실제 변환 길이 대신 ![]() 값을 정의합니다.
값을 정의합니다.
| 반지름(m) | 90 km/h | 100km/h | 110km/h | 120km/h | ||||
|---|---|---|---|---|---|---|---|---|
| E% |
|
E% |
|
E% |
|
E% | n/a | |
| 7000 | NC | n/a | NC | n/a | NC | n/a | NC | n/a |
| 5000 | NC | n/a | NC | n/a | NC | n/a | 2.0 | 0.31 |
| 3000 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.0 | 0.31 |
| 2500 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.0 | 0.31 |
| 2000 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.3 | 0.32 |
| 1500 | 2.0 | 0.39 | 2.0 | 0.34 | 2.2 | 0.33 | 3.0 | 0.33 |
| 1400 | 2.0 | 0.39 | 2.0 | 0.34 | 2.4 | 0.33 | 3.2 | 0.34 |
| 1300 | 2.0 | 0.39 | 2.0 | 0.34 | 2.6 | 0.33 | 3.5 | 0.34 |
| 1200 | 2.0 | 0.39 | 2.2 | 0.35 | 2.8 | 0.34 | 3.8 | 0.35 |
| 1000 | 2.0 | 0.39 | 2.6 | 0.36 | 3.7 | 0.35 | 4.5 | 0.37 |
| 900 | 2.2 | 0.40 | 2.9 | 0.37 | 3.7 | 0.36 | 5.0 | 0.38 |
| 800 | 2.5 | 0.40 | 3.3 | 0.38 | 4.2 | 0.38 | 5.7 | 0.39 |
| 700 | 2.9 | 0.41 | 3.7 | 0.39 | 4.8 | 0.39 | 6.0 | 0.40 |
| 600 | 3.4 | 0.42 | 4.4 | 0.41 | 5.6 | 0.41 | ||
| 500 | 4.0 | 0.44 | 5.2 | 0.43 | 6.0 | 0.42 | ||
| 400 | 5.0 | 0.46 | 6.0 | 0.45 | ||||
| 300 | 6.0 | 0.48 | ||||||
다음 예는 이전 테이블을 기반으로 두 가지 유형의 도로에 대한 접속 설치 방법과 공식을 보여 줍니다. 변수 {w}는 피벗점으로부터 이동 차선 모서리까지의 일반 도로 폭이며, 편경사 마법사에서 정의합니다.
<SuperelevationAttainmentMethod name="Unspiraled ramp">
<TransitionStyle style="Planar"/>
<Continuing>
<TransitionFormula type="NCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoBC" formula="{p}*{e}*{w}/{t}"/>
</Continuing>
<Opposing>
<TransitionFormula type="LCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoLC" formula="100*{c}*{w}/{t}"/>
<TransitionFormula type="LCtoRC" formula="100*{c}*{w}/{t}"/>
</Opposing>
</SuperelevationAttainmentMethod>
<SuperelevationAttainmentMethod name="Unspiraled 2 way roadway">
<TransitionStyle style="Standard"/>
<TransitionFormula type="LCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoLC" formula="100*{c}*{w}/{t}"/>
<TransitionFormula type="LCtoRC" formula="100*{c}*{w}/{t}"/>
<SuperelevationAttainmentMethod>