다음 단락에서는 CFD 방정식의 해를 구하는 것과 관련된 일부 수학적 용어의 정의를 제공합니다.
선형 - 비선형
지배 방정식이 다음 섹션에 나와 있습니다. 이러한 방정식에는 두 가지 유형의 비선형성이 나타납니다. 첫 번째 종류의 비선형성은 대류항으로 예시됩니다. 예를 들어, u 속도 방정식에는 다음과 같은 하나의 항이 나타납니다.
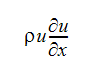
이러한 항에서 u는 u와 해당 도함수의 곱에 좌우됩니다. 지배 방정식에 나타나는 두 번째 유형의 비선형성은 항의 특성 또는 계수가 종속 변수에 좌우되는 경우입니다. 예를 들어, 에너지 방정식에서 밀도는 방정식에서 구하는 온도에 따라 좌우됩니다. 또한 속도 방정식에서 확산 항의 난류 흐름에 사용된 Eddy 점도는 속도에 따라 크게 좌우됩니다. 이러한 두 가지 유형의 비선형성은 지금까지 수치 솔루션에 지배적으로 영향을 미쳤습니다. 이런 이유로, 방정식은 반복 방식으로 해석해야 합니다.
명시적 - 암시적
항이 암시적으로 처리되면 계수 행렬의 일부가 되고, 결과적으로 솔루션의 일부가 됩니다. 항이 명시적으로 처리되면 최신 정보 대신 이전 반복 값이 사용됩니다. 이러한 항은 일반적으로 소스 항 또는 하중 벡터의 일부입니다. 이러한 항은 현재 반복 솔루션 후에 결정됩니다. 수치 안정성을 위해서는 가능한 많은 항을 암시적으로 처리하는 것이 좋습니다.
과도 해석의 경우 암시적 이산화 방법이 사용됩니다. 이 방법에서는 현재 시간의 값이 현재 시간의 인접한 값에 종속된다고 간주합니다. 명시적 이산화 방법에서는 현재 시간의 값이 이전 시간의 인접한 값에 종속된다고 간주합니다. 암시적 공식화는 수치적으로 무조건 안정적입니다. 즉, 시간 단계 크기에 관계없이 해를 구합니다. 그러나 각 시간 단계 내에 반복 솔루션이 필요합니다. 명시적 공식화는 조건부로만 수치적으로 안정적입니다. 시간 단계 크기 측면에서 종속성이 크고 제한적인 경우도 많습니다. 명시적 공식화를 위해 1.E-10초의 시간 단계를 사용하는 경우는 많이 있습니다. 그러나 각 시간 단계 내에서 솔루션을 반복할 필요는 없습니다.
대칭 - 비대칭
다음 섹션에 나오는 편미분 지배 방정식은 유한 요소를 사용하여 일련의 대수 방정식으로 이산화되며, 알 수 없는 값은 솔루션 변수의 절점 값이 됩니다. 이러한 대수 방정식은 다음과 같이 행렬 양식으로 작성할 수 있습니다.
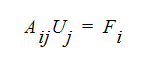
여기서 Fi는 하중 벡터이고 Uj는 알 수 없는 벡터이고 Aji는 계수 행렬입니다. 방정식의 대칭 시스템에서 A의 위쪽 대각선은 아래쪽 대각선의 대칭 이미지입니다. 예를 들면 다음과 같습니다.
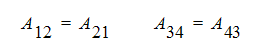
비대칭 시스템에는 해당되지 않습니다. 일반적으로 2차 도함수 항(예: 분산 항)은 대칭 행렬을 생성하고 1차 도함수 항(대류항)은 비대칭 행렬을 생성합니다.