분산 저항 모형

해석 특성

• 안정 상태
• 3D 내부 흐름
• 난류
• 비압축성 흐름
• 분산 저항 모형

참조

White, F.M., “Fluid Mechanics”, McGraw-Hill, New York, 1979, pp. 305-360

Idelchik, I.E., “Handbook of Hydraulic Resistance”, CRC Press, 1994, pp. 523

문제 설명

공기는 채널 중심에서 필터(또는 일부 흐름 장애물)을 사용하여 슬립 벽이 있는 3D 채널을 통해 흐릅니다. 벽에 슬립 조건이 있기 때문에 채널의 압력 강하는 장애물로 인한 것입니다.

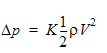
다음 4가지 분산 저항 모형이 모두 테스트되었습니다.

1. 일정한 K 계수:

K = 1.97748

지정된 압력 강하에서 이 K 계수로 인해 유량이 0.2m3/s입니다.

2. 파이프 마찰 손실:

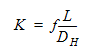
여기서 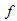는 Blasius 공식을 사용해 얻은 마찰 계수입니다. L = 41.99는 나타나는 파이프 길이이고, DH = 0.2는 파이프의 유압 지름입니다. 마찰 계수를 결정하는 데 사용된 Blasius 공식은 다음과 같습니다.

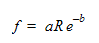
여기서 a는 0.316이고, b는 0.25입니다. 이러한 값에 따라 동일한 K-계수 값은 1.97748입니다. 따라서 유량으로 0.2m³/s를 예측할 수 있습니다.

3. 프리 영역 비율

이 저항 유형의 경우 Idelchik의 516페이지에 나와 있는 공식을 사용합니다.

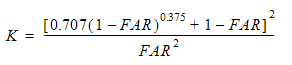
여기서 FAR은 프리 영역 비율입니다. 프리 영역 비율이 0.62이면 K 계수는 1.9774이고, 유량은 0.2m³/s입니다.

4. 헤드 손실 테이블의 K 계수:

다음 값 테이블을 사용합니다.

유량(m3/sec)	압력 헤드(Pa)
0.15	35000
0.25	45000

형상 및 경계 조건

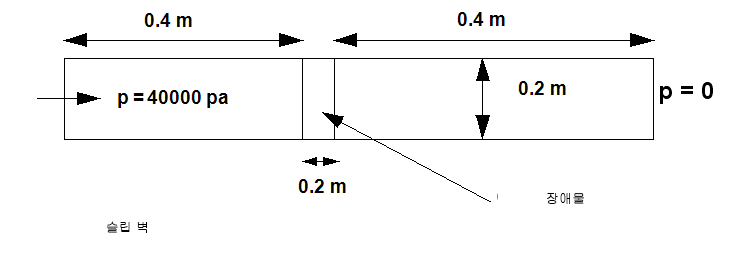
결과

분산 저항 유형	벤치마크	2016: 빌드 20150209	오류 비율	2017: 빌드 20160302	오류 비율
상수 K	0.2 m3/s	0.200387	0.193	0.1997	0.143
파이프 마찰 손실	0.2 m3/s	0.198389	0.805	0.2171	8.569
프리 영역 비율	0.2 m3/s	0.200388	0.193	0.1997	0.143
헤드 손실 테이블	0.2 m3/s	0.199279	0.360	0.1979	1.0475