이동 솔리드

이동 솔리드 모델링의 기본 개념은 비교적 단순합니다. 솔리드와 접촉하는 유체는 접촉점에서 순간 속도를 갖게 된다고 가정합니다. 즉, 이러한 상황에서는 슬립 없는 경계 조건을 적용합니다.

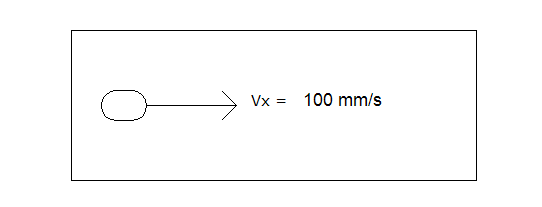
예를 들어, 아래의 스케치에서, 발사체는 초당 100mm로 왼쪽에서 오른쪽으로 이동합니다. 즉, 솔리드 표면을 따라 이동하는 유체에는 각 시간 단계에서 100mm/s의 속도가 지정됩니다.

임의 모션을 허용하기 위해 각 이동 부품 내에 로컬 좌표계가 배치됩니다. 부품은 이 로컬 좌표계를 기준으로 이동하지 않는 것으로 간주됩니다. 대신, 로컬 좌표계가 전역 좌표계를 기준으로 이동합니다.

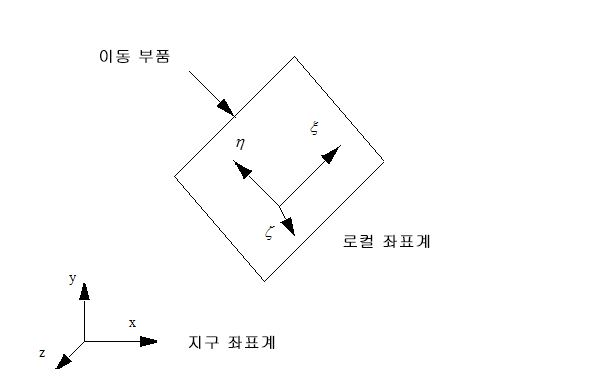
이동하는 부품에서 임의 점의 전역 좌표(x, y,z)는 다음 변환을 사용하여 계산할 수 있습니다.

여기서, (x, y, z)는 임의 시간(t)에 계산된 전역 좌표입니다.

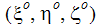• 는 로컬 좌표계 내에서 바라본 이동 부품의 좌표입니다. 이러한 좌표는 시간 0에서 1번만 계산됨을 나타내기 위해 위 첨자 o이 표시됩니다. 원칙적으로, 시간에 따라 달라지지 않습니다.
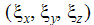• 는 로컬 x 축의 구성요소입니다.
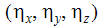• 는 로컬 y 축의 구성요소입니다.
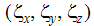• 는 로컬 z 축의 구성요소입니다.
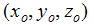• 은 로컬 좌표계 원점의 전역 위치입니다.

각 시간 단계에서 새 메쉬를 만들지 않고, 솔리드 메쉬가 유체 메쉬를 바로 통과하도록 허용됩니다. 유체 노드가 솔리드 요소로 "마스킹"되면 가장 가까운 솔리드 노드의 속도가 이 마스킹된 유체 노드에 적용됩니다. 다이어그램에서, 화살표로 표시된 유체 노드는 이동 부품 구석에 있는 솔리드 요소에 의해 마스킹됩니다. 이동 부품의 경계 내에 있는 모든 유체 노드는 "마스킹"된 것으로 간주되므로 해당 속도가 이동 솔리드에 의해 제어됩니다.

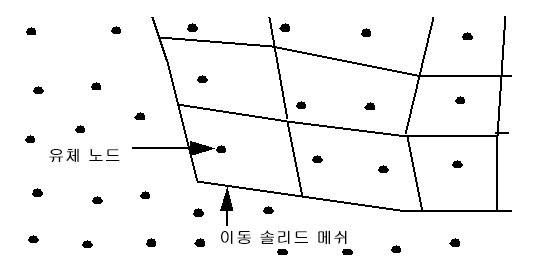
처음에 모형이 구성될 때 이러한 이동 솔리드는 여러 번 유체 내에 포함됩니다. 솔리드가 이동하기 시작하면 솔리드가 차지했던 영역에 유체 영역이 나타나야 합니다. 이러한 상황을 처리하기 위해 유체에 접하는 형태로 구성된 모든 솔리드에 유체 요소 및 노드가 자동으로 추가됩니다. 이 작업을 복제라고 합니다. 이동 솔리드가 유체 영역 외부에 위치하도록 모형이 구성되면 복제가 진행되지 않습니다.

선형 동작

선형 동작은 아래 그림과 같이 지정된 방향을 따라 기술됩니다.

변위(s)는 객체 시작 위치를 기준으로 측정됩니다. 사용자는 s를 궤적을 따라 객체를 이동하기 위한 시간 함수로 정의할 수 있습니다. 방향 단위 벡터(Ux, Uy, Uz)를 사용하여 궤적을 정의합니다. 전역 좌표계에서 정의된 모션은 다음과 같습니다.

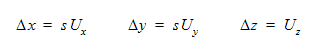
선형 동작이 흐름 구동인 경우, 전역 참조 프레임에서 계산된 전단 및 압력이 내적을 사용하여 s 방향으로 적용됩니다.

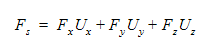
이 힘에 규정된 힘 및 스프링 힘을 추가할 수 있습니다. 모션 방정식은 다음과 같습니다.

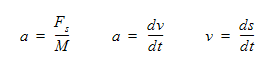
a는 가속도이고, M은 질량이고, v는 속도이고, s는 변위이고, t는 시간입니다.

회전 동작

회전 동작의 경우, 아래 그림과 같이 축을 따라 회전하는 객체가 있습니다.

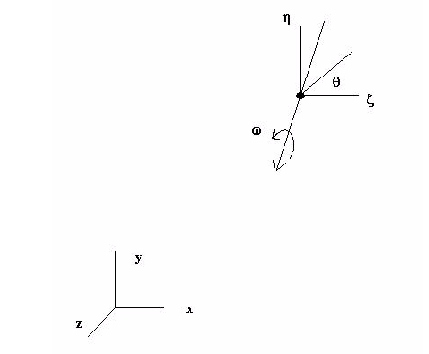
객체가 회전하는 축은 단위 벡터(U_x, U_y, U_z)를 사용하여 정의합니다. 회전의 중심은 점(P_x, P_y, P_z)에 지정됩니다. 각도 측정은 변수 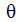를 사용하여 수행합니다.

각도는 이동하는 객체의 시작 위치를 기준으로 측정합니다. 로컬 좌표계에서는 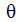대 시간을 사용하여 동작을 기술할 수 있습니다.

3D 표현의 경우 방향 코사인을 사용하여 동작을 나타내는 것이 편리합니다.

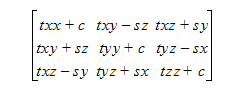
여기에서

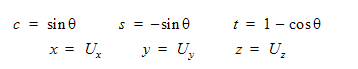
모션이 흐름 구동인 경우 회전 축에 작용하는 토크는 내적을 통해 계산됩니다.

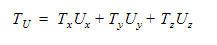
사용자 규정 토크도 이 토크에 추가할 수 있습니다. 동작 방정식은 다음과 같습니다.

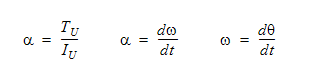
여기서 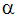는 각가속도이고, I_u는 회전 벡터에 대한 회전 관성이고, 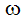는 각속도이고, 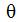는 각도 위치이고, t는 시간을 나타냅니다.

결합된 선형 및 회전 동작

이전 두 섹션의 결과를 결합하면 결합된 동작을 기술할 수 있습니다. 이제 회전 중심이 s로 지정된 경로를 따라 정의된 대로 변환됩니다. 다시 말해서 회전은 로컬로 기술되고, 방향 코사인은 전역으로 기술됩니다. 선형 변환이 흐름 구동인 경우 유체 힘이 이동 방향을 따라 힘 벡터를 증가시키고 선형 가속이 발생합니다.

흐름 구동 회전의 경우 증가된 토크를 사용해서 각가속도를 계산합니다. 두 동작이 모두 흐름 구동인 경우 두 동작은 커플링되지 않고 독립적으로 작동하여 전체 동작을 생성합니다. 선형 변환 방정식은 시간에 따라 회전 중심을 업데이트하고, 회전 방정식은 시간에 따라 방향 코사인을 업데이트하여 결합된 동작을 생성합니다.

궤도 및 회전 동작

궤도 동작에서는 객체가 시간에 따른 순환 경로로 이동합니다. 해당 상황은 아래 그림에 표시되어 있습니다.

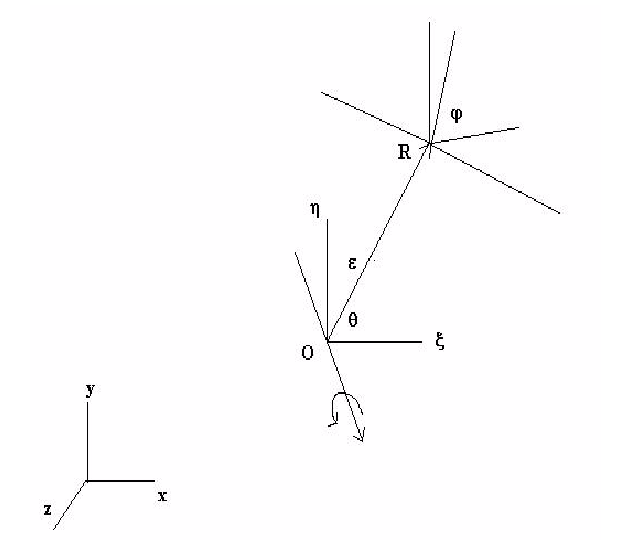
변수 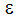은 궤도 반지름 또는 편심입니다. 이 변수는 점 O와 점 R을 사용하여 계산됩니다.

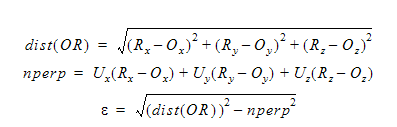
여기서는 수직이 아닌 벡터를 빼서 궤도 시스템의 원점과 회전 시스템의 축 간 수직 거리를 구했습니다. 벡터(U_x, U_y, U_z)는 궤도 시스템에 대한 회전 축을 설명하는 단위 벡터입니다.

로컬 좌표계에서 궤도는 다음으로 지정됩니다.

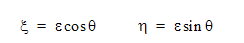
이것은 다음과 같이 회전 변환 행렬을 구성하여 전역 참조 프레임에 나타낼 수 있습니다.

1. 로컬 z축(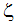)은 궤도 축 U와 같습니다.
2. 로컬 x축(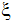)은 궤도 시스템의 원점에서 시간=0 회전 시스템 원점을 가리키는 단위 벡터로 구성됩니다.
3. 로컬 y축(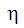)은 로컬 z축과 로컬 x축을 교차하여 구성됩니다.
4. 일단 모든 로컬 축이 정의되면, 이 로컬 시스템이 진정한 직교가 되도록 하기 위해 Gram-Schmidt 절차가 진행됩니다.

의 함수인 전역 궤도 위치를 다음과 같이 작성할 수 있습니다.

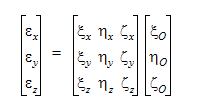
궤도 동작이 흐름 구동인 경우 움직이는 객체에 작용하는 힘이 합산되고 해당 가속도가 계산됩니다. 속도 및 변위는 다음 관계를 사용하여 원형 궤도 경로로 제한됩니다.

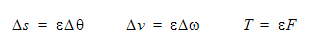
동작의 궤도 방정식이 이동 객체의 변환을 정의합니다. 편심 벡터가 가리키는 점에서도 객체가 회전할 수 있습니다. 이전에 개발된 회전 방정식이 이 동작을 지배합니다.

장동 동작

장동 동작은 아래 그림을 사용하여 설명할 수 있습니다.

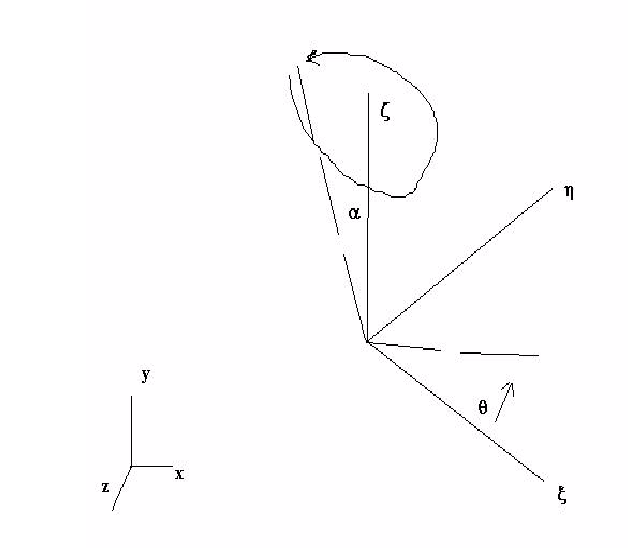
세차 또는 장동 각도는 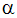와 같이 정의됩니다. 각도 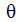는 로컬 z 축을 기준으로 각도 이동을 정의합니다. 로컬 y축입니다[중지가 로컬 y 및 z 평면의 동작을 허용하는 위치(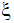= 0) 정의]. 로컬 공간에서 방향 코사인은 다음과 같습니다.

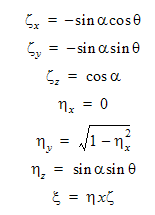
이전과 마찬가지로 회전 변환 매트릭스가 전역 공간에서 방향 코사인을 작성하는 데 사용됩니다.

장동 모션이 흐름 구동이면, 순 토크를 사용하여 앞서 설명한 회전 본체에 대해 수행한 것과 같은 방식으로 각가속도를 계산합니다.

자유 모션

이 유형의 모션은 여기에 설명된 구속되지 않은 강체 역학 공식을 사용합니다.