유체 흐름 및 열 전달에 대한 지배 방정식은 Navier-Stokes 또는 운동량 방정식 및 열역학 제1법칙 또는 에너지 방정식입니다. 지배하는 PDES를 다음과 같이 작성할 수 있습니다.
연속성 방정식:
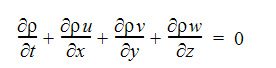
X-모멘텀 방정식:
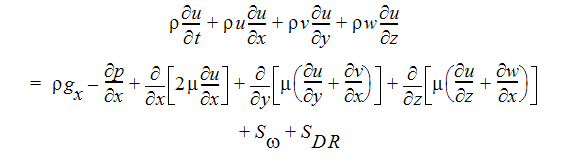
Y-모멘텀 방정식:
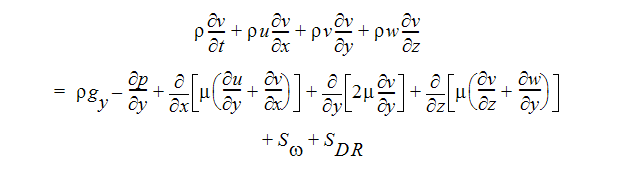
Z-모멘텀 방정식:
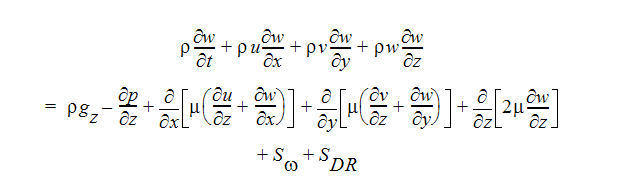
운동량 방정식의 두 소스 항은 각각 좌표 회전 및 분산 저항에 대한 것입니다. 분산 저항 항은 일반적으로 다음과 같이 작성할 수 있습니다.
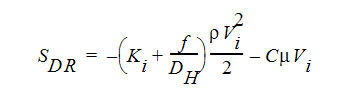
i는 전역 좌표 방향(u, v, w 운동량 방정식)을 나타냅니다. 다른 항에 대한 설명은 이전 섹션을 참조하십시오. 각 방향에는 고유한 K-계수가 있으므로 한 번에 단일 운동량 방정식에서 K 계수 항이 작동할 수 있습니다. 다른 두 개의 저항 유형은 각 운동량 방정식에서 동일하게 작동합니다.
다른 소스 항은 흐름 회전에 대한 것입니다. 이 항은 일반적으로 다음과 같이 작성될 수 있습니다.
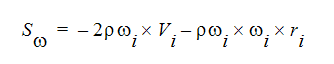
i는 전역 좌표 방향을 나타내고 
은 회전 속도이고, r은 회전 축에서의 거리입니다.
비압축성 및 아음속 압축성 흐름의 경우 에너지 방정식이 정적 온도 항으로 작성됩니다.
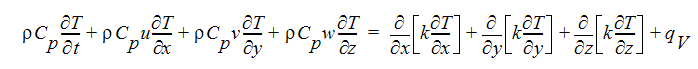
다중 위상 흐름(예: 증기/물)의 경우 에너지 방정식은 엔탈피 항으로 작성됩니다.
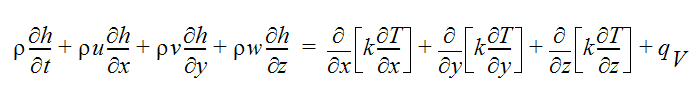
CFdesign 버전 9.0 이전에는 엔탈피 기반 공식을 사용해서 습도 계산을 수행했습니다. 이 경우 유체의 엔탈피는 습도(증기 또는 액체 상태)와 공기 또는 운반 가스의 에너지를 나타냅니다. 그러나 이후 버전에서는 위상 변경을 고려하기 위해 습한 가스 흐름에 비열을 특수하게 취급하는 온도 기반 공식이 사용됩니다.
다중 위상의 물 흐름의 경우 엔탈피는 증기 및 액체 위상에 대한 에너지입니다.
압축성 흐름의 경우 에너지 방정식은 총 온도 항으로 작성됩니다.
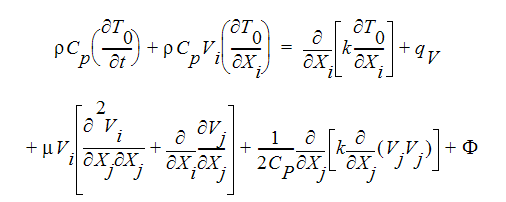
여기서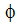 
는 산일 함수입니다. 간결하게 나타내기 위해 총 에너지 방정식에는 아인슈타인 텐서 표기 방식이 사용되었습니다. 마지막 세 항은 압축성 흐름에만 존재합니다.
이러한 방정식의 변수는 아래 테이블에 정의되어 있습니다.
| 변수 | 설명 |
| Cp | 상수 압력 비열 |
| gx, gy, gz | x, y, z 방향의 중력 가속 |
| h | 엔탈피 |
| k | 열 전도율 |
| p | 압력 |
| qV | 체적 열 소스 |
| T | 온도 |
| t | 시간 |
| u | x 방향의 속도 구성요소 |
| v | y 방향의 속도 구성요소 |
| w | z 방향의 속도 구성요소 |
|
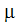
점도 |
|
밀도 |
연속성, 모멘텀 및 에너지 방정식은 5개의 미지수 u, v, w, p, T 또는 To의 5개 방정식을 나타냅니다. 이러한 방정식은 직교 형상에 대해 안정 상태 조건에 있는 유체 흐름 및 열 전달을 설명합니다.
소용돌이 속도 구성요소(평면외 구성요소)가 있는 축대칭 형상 및 안정 상태 조건의 경우 이러한 방정식을 다음과 같이 작성할 수 있습니다.
연속성 방정식:
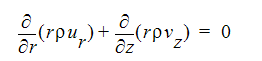
R-모멘텀 방정식:
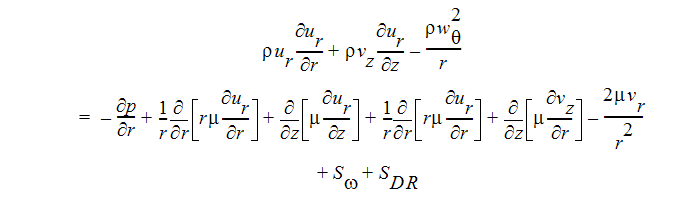
Z-모멘텀 방정식:
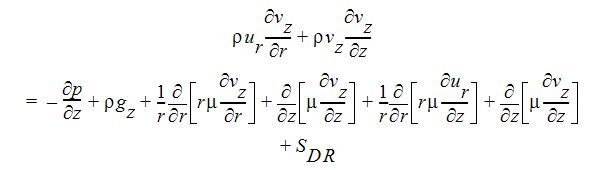
소용돌이 속도 방정식:
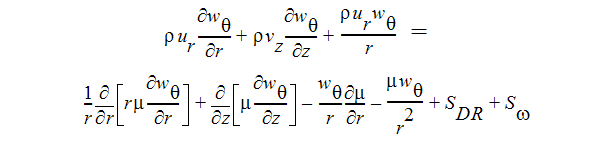
에너지 방정식에는 축대칭 흐름에 대한 추가 항이 없습니다.