다음 방정식은 비압축성 유체를 통과하는 수동 스칼라의 전송을 설명합니다.
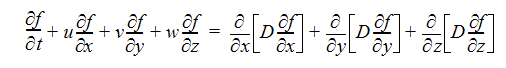
이 방정식에서 변수는 다음 표에 정의되어 있습니다.
| 변수 | 설명 |
| D | 확산 계수(길이2/초) |
| f | 수동 스칼라 |
| t | 시간(초) |
| u | x 방향의 속도 구성요소(길이/초) |
| v | y 방향의 속도 구성요소(길이/초) |
| w | z 방향의 속도 구성요소(길이/초) |
Autodesk® CFD에서 종류 확산 계수(D)를 해석 > 고급 대화상자에 입력합니다. 확산 계수 단위는 길이의 제곱을 시간으로 나눈 것입니다(예: m2/초).
난류 흐름에서 위의 방정식은 시간 평균으로, 스칼라 변수를 평균값 및 변동 값의 중첩으로 나타낼 수 있다고 가정합니다. 여기서 변동은 평균값에 대한 것입니다. 예를 들어 스칼라 변수는 다음과 같이 작성할 수 있습니다.
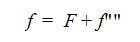
여기서 F는 평균 스칼라 값이고 f""는 이 평균값에 대한 변동입니다. 이 표현은 지배 방정식으로 대체되고, 시간이 흐름에 따라 방정식에 대한 평균이 계산됩니다. 대문자가 평균값을 나타내고 소문자가 변동 값을 나타내는 표기법을 사용하여 평균을 구하는 난류 스칼라 방정식을 다음과 같이 작성할 수 있습니다.
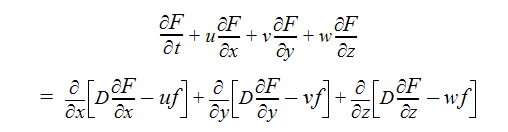
이 평균화 프로세스는 스칼라 방정식에 추가 항 
uf, vf 및 wf를 생성합니다. 이러한 항은 비선형 관성 또는 이류 조건에서 구한 평균과 변동 수량을 조합한 것입니다.
이제 이러한 추가 항을 "모델링"할 메서드를 찾아야 합니다. 즉, 이러한 항을 이전에는 알 수 없었던 평균값에 다시 연결합니다. 0번째 마감 레벨에서 추가 항은 다시 종속 변수 F에 연결됩니다.
운동량 방정식에 대해 마감과 동일한 레벨을 사용하여 Eddy 확산 계수를 정의하는 Boussinesq 근사를 적용합니다.
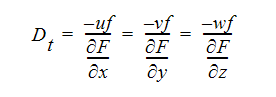
이러한 정의를 평균 스칼라 방정식에 사용하는 경우 결과는 다음과 같습니다.
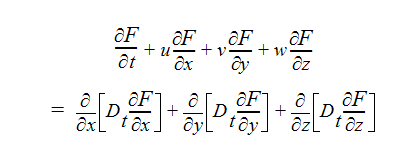
이 경우 Eddy 확산 계수 Dt만 결정해야 합니다.
Eddy 확산 계수는 Eddy 점도 및 난류 Schmidt 번호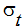 
를 사용하여 계산됩니다.
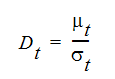
난류 Schmidt 번호는 일반적으로 1.0이 됩니다.
경계 조건
스칼라 방정식에 적용해야 하는 조건에는 입구, 출구, 슬립이 발생하지 않는 벽, 대칭 선, 슬립 벽 및 주기적 경계의 6가지 유형의 경계가 있습니다. 입구의 경우 값이 0이더라도 스칼라 값을 지정해야 합니다. 출구, 대칭 선 슬립 벽 및 슬립이 발생하지 않는 벽에서 스칼라 방정식은 경계에 수직인 제로(0) 그라데이션의 자연 경계 조건을 사용합니다. 주기적 경계에서 한 경계의 스칼라는 다른 주기적 경계의 해당 점에 적용되거나 해당 점으로 변환됩니다.
일반 스칼라를 사용하여 연소 시뮬레이션
스칼라 전송 방정식을 사용하여 연소를 대략적으로 시뮬레이션할 수 있습니다. 연소 진행 속도를 제한할 수 있는 다음과 같은 세 가지 프로세스가 있습니다.
- 매크로 혼합 - 연료 및 산화제의 큰 Eddy가 대류성 및 확산성 전송 메커니즘의 작동에 따라 결합하거나 상호 작용합니다.
- 마이크로 혼합 - 연료의 분자가 산화제의 분자와 접촉합니다.
- 반응 속도론 - 산화제에 반응하는 연료의 실제 화학 공정은 여러 중간 종류를 포함한 일련의 화학 반응에 따라 제어됩니다. 이러한 반응 속도는 존재하는 종류와 로컬 온도에 의해 결정됩니다.
이 중 속도가 가장 느린 프로세스가 주로 연소 프로세스의 진행률을 결정합니다. 속도가 1 또는 2로 구속된 연소 프로세스를 "혼합 제한"이라고 합니다. 이 경우에는 "혼합되면 연소된다"고 가정합니다. 이와 같은 혼합 제한의 경우 연료 및 산화제가 화학량론 비율에서 항상 반응하여 연소로 인한 주요 부산물을 형성한다고 가정합니다. 중간 종류는 무시됩니다. 예를 들어 일반 연료에 대한 화학량론 반응은 다음과 같은 방정식으로 작성할 수 있습니다.
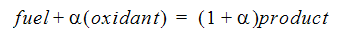
여기서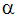 
는 1 단위 질량의 연료를 태우는 데 필요한 화학량론 계수입니다.
연료 및 산화제는 다음과 같이 단일 스칼라 변수로 결합할 수 있습니다.
-
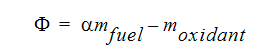
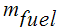은 연료의 질량 분율입니다. 즉, 연료의 질량을 연료와 산화제를 더한 총 질량으로 나눈 값입니다. -
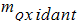는 산화제의 질량 분율입니다.
이 스칼라 변수는 안정 상태 계산에서(소스 또는 싱크 항 없음) 대류 및 확산 이동 균형과 같은 보존량이 됩니다.
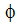에 대한 전송 방정식은 다음과 같이 동일한 교환 계수(확산 계수)를 가정하여 연료 종류 전송 방정식에서 산화제 종류 전송 방정식을 곱한 것을 빼서 파생됩니다.
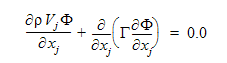
이 방정식에서 첫 번째 항은 대류항이고 두 번째 항은 확산성 항입니다. 새로 정의된 이 스칼라 변수를 사용하여 혼합 분율을 다음과 같이 정의할 수 있습니다.
-
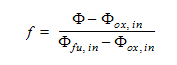
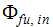은 연료 입구 스트림에서의 스칼라 값입니다. -
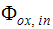은 산화제 입구 스트림에서의 스칼라 값입니다.
혼합 분율의 이 정의를 사용하는 경우 f 값은 연료 스트림에서 1.0이고, 산화제 스트림에서는 0.0입니다.
화학량론 조건에서 f 값은 fst로 표시됩니다.
f가 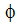값의 선형 조합이므로 f는 또한 보존량입니다. 따라서 f에 대한 전송 방정식을 다음과 같이 작성할 수 있습니다.
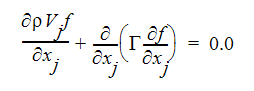
연료 및 산화제가 만났을 때 화학적 평형을 가정하면 연료 및 산화제의 질량 분율은 다음과 같이 계산할 수 있습니다.
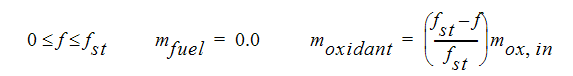
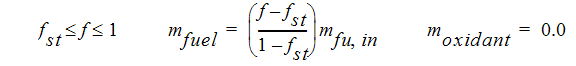
제품의 질량 분율은 이러한 두 방정식의 나머지 부분에서 결정할 수 있습니다.