이산 프로세스는 모든 노드에서 대수 방정식을 생성합니다. 이러한 방정식은 매트릭스, Aij를 형성합니다. 이 매트릭스에는 노드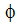 
값에 대해 0이 아닌 계수를 포함하기에 충분한 유한 요소 노드와 열만큼의 행이 있습니다.
매트릭스 방정식을 푸는 고전적 방법은 가우스 소거법입니다. 제거 프로세스를 수행하려면 분해 중에 생성된 채우기를 위해 띠 매트릭스가 하나 이상 필요하므로 이 방법은 솔루션을 얻는 데 다소 비용이 많이 듭니다. Autodesk® CFD에서 저장한 Aij는 밴드 매트릭스보다 훨씬 작습니다. 또한 제거 프로세스는 컴퓨팅 집약적입니다. 이러한 방정식을 반복해서 풀기 때문에 비용이 많이 드는 이 제거 절차는 너무 느리고 지루할 수 있습니다.
제거 기술 사용의 대안으로는 반복적인 매트릭스 솔버 사용이 있는데, 이 방법에서는 계산 횟수를 줄이고 채우기 프로세스를 완전히 제거하도록 근사치가 구성되어 있습니다. 따라서 0이 아닌 매트릭스 항목만 필요하므로 컴퓨터 스토리지 요구 사항이 크게 줄어듭니다(3D 문제의 20~30배 크기). 특히 생성 중인 근사치는 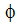의 이전 값을 현재 값의 예측 값으로 사용할 수 있습니다. 반복 패스 또는 솔버 전체에서 반복한 결과는 가우스 소거법 기술에서 반올림 오차를 뺀 것과 동일한 솔루션을 생성합니다. 하지만 방정식의 비선형 특성으로 인해 이 시점에 도달하기 전에 반복을 중지하려고 할 수 있습니다.
가장 간단한 반복 매트릭스 솔버는 다음 방정식으로 값이 결정되는 Gauss-Seidel 절차입니다.
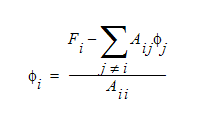
이 방정식에서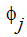 
값은 가장 최근에 사용 가능한 값입니다. 실제로 이렇게 하면 모든 비대각 항이 방정식의 오른쪽으로 전송됩니다. 적절한 솔루션에 도달하기 위해 수행하는 Gauss-Seidel 반복 횟수가 꽤 크므로 이 방법은 자주 사용되지 않습니다.
특히, 전송 문제에 대해 Gauss-Seidel보다 훨씬 향상된 솔루션을 제공하는 다른 반복형 매트릭스 솔버는 TDMA(Tri-Diagonal Matrix Algorithm)입니다. 이 방법에서는 3대각 행렬 계산식이 구성됩니다. 여기서 계수 매트릭스의 대각선에 인접한 두 열이 유지되고, 다른 두 항은 í의 기존 값을 사용하는 방정식의 오른쪽으로 전달됩니다. TDMA에 대한 매트릭스 방정식은 다음과 같이 작성할 수 있습니다.
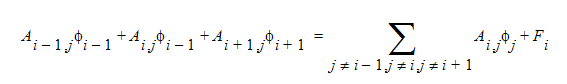
TDMA 알고리즘은 노드의 1차원 평면을 동시에 효과적으로 해석합니다. 전송 방정식에서 정보는 입구 평면에서 각 연속 평면으로 전달됩니다. 따라서 TDMA 알고리즘을 사용하여 전송 방정식을 해석하는 것은 이 물리적 정보 흐름 프로세스를 모방합니다.
공액 기울기법의 변형인 여러 가지 반복 매트릭스 솔버가 있습니다. 일부 방법은 비대칭 매트릭스에만 적용 가능하고, 그 외에는 비대칭 매트릭스에 적용합니다. 이러한 변형은 모두 유사한 기술을 사용하여 매트릭스 방정식을 풉니다. 즉, 검색 기법을 사용하여 직접 매트릭스 방정식 및 수렴 해석을 빠르게 수행합니다. 이러한 변형은 매우 정확한 해석을 생성하므로 일반적으로 반직접 매트릭스 솔버라고 합니다. Autodesk® CFD에서 공액 기울기법 솔버는 수렴 조건이 충족되거나 사용자가 설정한 반복 수가 초과될 때까지 제거 프로세스를 통해 반복됩니다.