Сосредоточенная сила, приложенная в точке по длине стержня, действует вдоль продольной оси стержня. Для простоты определения сосредоточенных сил, приложенных в точках, не лежащих на продольной оси стержня, можно задать значение эксцентриситета сил по отношению к продольной оси стержня.
Нагрузки с эксцентриситетом приводятся к оси стержня.
На следующем рисунке показан основной случай приведения нагрузки к оси стержня в пространственной конструкции.
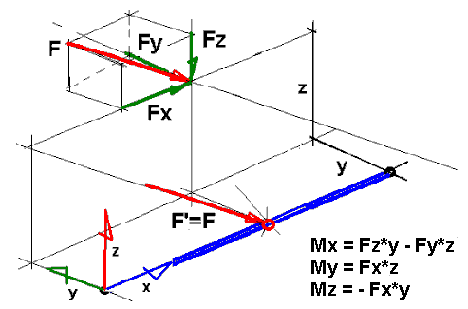
Ниже даны некоторые комментарии, относящиеся к нагрузкам с эксцентриситетом.
- Сосредоточенный момент, приложенный с эксцентриситетом, не вызывает никаких дополнительных сил при его приведении к оси стержня.
- Каждая сосредоточенная сила, приложенная с эксцентриситетом, приводится к точке x
0
на оси стержня с тем же значением F и с тем же направлением действия. Дополнительно в точке x
0
прикладывается момент силы относительно этой точки. Компоненты приложенной с эксцентриситетом сосредоточенной силы в локальной системе координат стержня Fx, Fy, Fz приводятся к точке x0 без изменения. Дополнительные моменты относительно осей локальной системы координат вычисляются так:
Mx = Fz*y - Fy*z;
My = Fx*z;
Mz = - Fx*y.
- Равномерно распределенная нагрузка интенсивности р, приложенная с эксцентриситетом по всей длине стержня, приводится к оси стержня без изменения величины p и направления ее действия. Дополнительно по всей длине стержня прикладывается равномерно распределенный момент. Как и в случае сосредоточенных сил, если приложенная с эксцентриситетом равномерно распределенная нагрузка задана компонентами px, py, pz в локальной системе осей стержня, то она приводится к оси стержня в виде равномерно распределенной нагрузки с теми же компонентами и дополнительных равномерно распределенных моментов вида:
mx = pz*y - py*z;
my = px*z;
mz = - px*y.
Прим.: В зависимости от типа конструкции применяются следующие ограничения:
- В плоских конструкциях (плоская рама, плоская ферма) эксцентриситет определяется только в направлении z. В это время поле y недоступно в диалоговом окне. Основное правило заключается в том, что в двумерных конструкциях, работающих на поперечную нагрузку, в локальной системе осей отсутствует угол поворота вокруг оси z – угол гамма. Это правило касается и нагрузок, приложенных с эксцентриситетом: при приведении нагрузок к оси стержня появляется лишь один дополнительный момент My= Fx*z.
- Для таких типов двумерных конструкций, как ПЛИТА и БАЛОЧНАЯ КЛЕТКА, эксцентриситет определяется для направлениий y и z . Основное правило заключается в том, что в двумерных конструкциях в локальной системе осей отсутствует угол поворота вокруг оси z – угол гамма. Это правило касается и нагрузок, приложенных с эксцентриситетом. Генерируются только моменты Mx= Fz*y - 0*z.