超弹性和泡沫材料模型的材料属性输入对话框提供了一个“曲线拟合”例程。通过对用户提供的材料应力-应变数据执行最佳拟合计算,曲线拟合可用于确定数学材料模型的常数。请记住,任何解均无法准确拟合测试数据!测试和材料中的变化将导致测试数据散布。因此,在大多数情况下,曲线拟合例程无法达到较高的精度。重要的是,曲线拟合例程的结果取决于所需范围内的测试数据。
每个材料模型均有一些与自身需求特定相关的选项。根据具体的材料模型,以下描述的某些项可能无关。“曲线拟合”对话框的常规布局如图 1 中所示。下面我们将逐一描述。
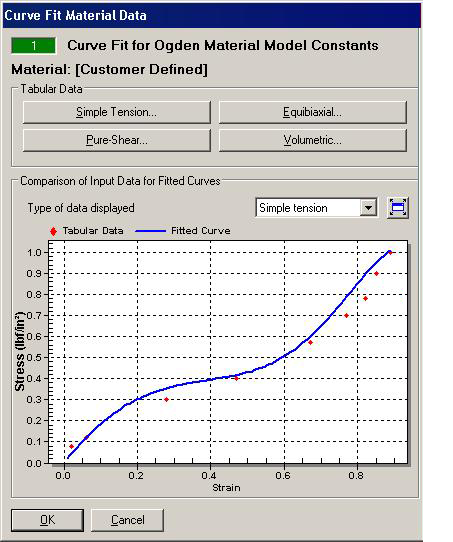
图 1(左):Ogden 的“曲线拟合”对话框(对话框的左半部分)

图 1(右):Ogden 的“曲线拟合”对话框(对话框的右半部分)
“表格数据”部分:
此部分用于输入材料的已知应力-应变数据。首先,获取测试数据时务必记住以下几点:
- 若要得到精确的分析常数,“曲线拟合”中输入的应力-应变数据必须涵盖分析中将遇到的完整载荷范围。例如,如果部件除了拉伸和压缩以外,还会遇到剪切应力,则必须输入“纯剪切”应力-应变数据。“简单拉伸”本身不足以对这些情况下的材料行为进行建模。这一点同样适用于其他类型的表格数据。
- 由于需综合使用所有各种体验的数据才能得到材料常数,因此测试材料必须来自同一批次,这一点至关重要。否则,材料生产中的变化将导致测试数据倾斜。
- 许多弹性体在前几个载荷循环期间会改变其行为。此外,当遇到的最大应变增加时,应力-应变曲线也会有所变化。因此,材料应不断循环,以达到分析中所需的应变值;载荷应不断重复,直到行为稳定为止。
- 如果未提供此类数据,则应力-应变测试数据可能需要转移到零应变条件。超弹性材料拉伸到新的应变率之后,通常不会返回原始应变。(无论是经历第一次循环还是多次循环,均是如此;更高的新应变率将导致新的永久变形。)测试中测量得出的永久变形需从应变值中删除。同样,因永久变形导致的横截面面积变化必须体现在计算应力所使用的初始面积中。这两种修正方法会将应力-应变曲线重新移回至起始值 0,0。
- 根据使用的材料模型,大多数超弹性材料模型不会更改因重复载荷造成的属性。分析中的每个循环均遵循计算得出的应力-应变曲线。因此,可能需要选择测试数据或取其平均值,才能匹配分析行为。
- 大多数超弹性材料模型均遵循相同的应力-应变加载和卸载曲线。不存在永久变形。
您可输入的测试数据类型如下所示:
- “简单拉伸”按钮:输入简单拉伸测试中的应力-应变数据。必须提供这类测试数据,才能测量纯拉伸应变状态。测试数据中不存在侧向约束。仅需输入拉伸分叉。压缩数据从等双轴数据中得出。
- “等双轴”按钮:输入等双轴拉伸测试中的应力-应变数据。这是用于重现压缩应力-应变的测试数据。通过在两个方向上均匀拉伸,创建相当于纯压缩的应变状态。
- “纯剪切”按钮:输入纯剪切应变测试中的应力-应变数据。对于超弹性材料,这通常是指大幅拉伸的样品,但由于该材料几乎不可压缩,因此存在纯剪切状态。
- “简单剪切”按钮:输入简单剪切测试中的应力-应变数据。
- “体积”按钮:输入体积压缩测试中的压力-应变数据。此数据用于确定体积模量。对于超弹性材料,如果材料可稍加压缩或部件十分受约束,则此数据非常重要。体积模量通常比剪切模量大两到三个数值阶次。对于泡沫材料,体积数据对捕获泡沫的可压缩性十分重要。
单击“表格数据”部分中的任一按钮,将弹出一个新对话框。在此对话框中,您可输入应力和应变数据。可用的控件如下所示:
- “应变格式”下拉菜单:选择应变数据的格式。“额定”应变的计算公式为(长度变化)/(原始长度),“拉伸”的计算公式为(当前长度)/(原始长度)= 1+ (额定应变)。
- “有效的泊松比”字段(仅限泡沫材料模型):如果泊松比已知、但横向应变未知,则输入有效的泊松比值。结合使用此输入与“填充”按钮和电子表格中输入的主应变,以计算横向应变。
- “填充”按钮:单击此按钮将计算应变值。电子表格中的“横向”列基于“有效的泊松比”字段和“应变,主要”电子表格列。
- “输入横向应力”复选框:对于泡沫材料,剪切应力和横向应力可以具有不同的值。如果激活此选项(仅在“简单剪切”测试数据中显示),则应在应力-应变电子表格中输入横向剪切应力。如果未激活此选项,则系统将假定横向剪切应力等于该剪切应力,且电子表格中不显示该列。
- “应力-应变数据”或“体积压力-应变数据”电子表格:输入所需的应力和应变(取决于数据类型)。应使用工程应力和应变(根据原始长度和面积)。应根据第二列(通常为超弹性材料的应变和泡沫材料的应力)按升序输入这些值。
- “自动更正”复选框:对于体积压力-应变数据,应变和压力的符号必须正确无误,才能计算得出正确的体积模量。如果激活此选项,处理器将根据需要切换输入体积压力的符号,以获得正确的计算结果。如果未激活,则应变值应为负,压力应为正。
- “添加行”和“删除行”按钮:分别在电子表格的末尾添加行和删除当前行。
- “排序”按钮:根据第二列(通常为超弹性材料的应变值或泡沫材料的应力值)按升序对应力-应变数据进行排序。
- “导入”按钮:从逗号分隔文件 (CSV) 导入应力-应变数据。数据文件的格式应与电子表格相同,但不含“索引”列。请注意,所有现有数据均会替换为导入的数据。对于泡沫材料模型,可以导入两列或三列。如果逗号分隔值文件中没有第三列“应变,横向”,则该列将设置为零。使用“有效的泊松比”字段和“填充”按钮可创建估计值。 注意: 有些应力-应变电子表格在第一列中使用应力,也有些使用应变。.CSV 文件必须具有适当的列数据,与电子表格对应。提示: 逗号分隔文件中的值通过使用活动的“显示单位”导入。导入数据之前,您可根据需要更改“显示单位”。例如,如果“显示单位”设置为磅和英寸,则值 314 导入为 314 psi;如果“显示单位”为牛顿和米,则导入为 314 Pa。
- “导出”按钮:将输入的应力-应变数据保存到逗号分隔文件中。
“参数”选项卡
某些材料模型需要估计值或猜测值才能启动最小二乘法拟合例程。这些参数是在“参数”选项卡中输入的,且应在尝试曲线拟合之前提供。具体输入哪些参数,这取决于您在“控制”选项卡中选择的曲线拟合方法算法。
“部分线性最小二乘法”:此搜索方法根据初始猜测计算所有可能的系数组合,并报告误差最小的组合。由于这种方法将计算所有组合,因此可能比其他方法所需的时间更长,特别是当使用较大的增量值时尤其如此。另请注意,超出范围的解不会测试,因此可能存在误差较小的解。如果绘制的结果与数据不符,请尝试使用其他范围。输入如下:
- “估计”或“猜测”值:输入参数的初始估计值或猜测值。此输入实际上是计算范围的中间值。请注意,对于部分材料模型中的某些值,可能无法接受值 0。例如,Ogden 材料模型的电位方程在分母中使用参数 Alpha,因此不接受除零。如果在拟合例程期间出现这种情况,则该参数将切换为预定义的默认值。
- “范围值”:输入测试的猜测值范围(测试的最低值到最高值)。最低值等于猜测值减去范围的一半,最高值等于猜测值加上范围的一半。
- “增量”值:这是计算得出的最低值与最高值之间的点数。因此,如果有三个参数且其增量为 20,则可创建 20^3 = 8000 个报告最小误差的组合。
“Levenberg-Marquardt 算法”、“Gauss-Newton 算法”和“受约束的优化”:这些方法从初始猜测开始计算,并找到最佳拟合方程的第一个最小值(误差函数的斜率为零)。由于涉及多个变量时可能存在若干最小值,因此解的精度取决于初始猜测。请参见图 2。
- “估计”或“猜测”值:为每个常数输入所需的估计值或猜测值。最好不要使用值零。此外,应根据模型的阶次为每次猜测输入一个非零值。如果计算 5 阶模型,则应为前 5 个常数输入估计值。较好的估计值源自另一曲线按拟合方法。例如,使用“部分线性最小二乘法”方法找到的常数是 Levenberg-Marquardt 算法的较好估计值。由于曲线拟合是一种数值求解技术,因此不同的估计值可能会产生不同的曲线拟合结果。
- “最大迭代次数”字段:输入要使用的最大迭代次数。如果在达到最大迭代次数之前未得出解,则曲线拟合例程期间将显示错误。
- “容差”字段:输入要用于曲线拟合例程的容差。如果每个常数在不同迭代之间的变化值小于容差,则其解视为收敛。
误差
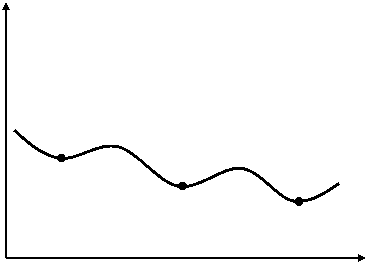 值
值
“控制”选项卡
“曲线拟合控制”部分:
曲线拟合控制用于指示如何将测试数据用于曲线拟合例程(例如,曲线拟合计算中使用哪些测试数据)、模型阶次和数据拟合方法。
- “使用数据”复选框:对于曲线拟合例程中要使用的测试数据,激活这些复选框。输入的所有测试数据均应使用。对于某一组特定的数据,只有一种原因可以不使用,即:该组数据将导致很难拟合其他数据。在这种情况下,应使用不同的模型阶次、不同的曲线拟合方法或材料模型,以获得更好的拟合效果。
- “曲线拟合方法”下拉菜单:选择一种数值技术,以查找测试数据的最佳拟合。每种技术均会提供一组不同的常数。能够有效拟合数据(从可视化角度和 RMS 角度)的方法便是要使用的方法。请注意,“Levenberg-Marquardt 算法”和“Gauss-Newton 算法”可能需要初始估计值;请在“参数”选项卡中输入这些值。“部分线性最小二乘法”方法适用于查找常数的初始估计值。
- “模型阶次”下拉菜单:选择曲线拟合例程的模型阶次。通常,阶次越低,分析速度就越快更快;但若要更好地拟合测试数据,则需使用阶次较高的模型,特别是当应力-应变曲线较弯曲时尤其如此。
- “体积模量阶次”下拉菜单:选择曲线拟合例程的体积模量计算阶次。阶次越高,测试数据的拟合精度越高。除非提供体积测试数据,否则某些材料模型无法估计此值;除非在曲线拟合中输入并使用体积测试数据,否则其他材料模型会将此输入默认为 1 阶常数。
- “执行曲线拟合”按钮:单击此按钮可开始曲线拟合操作。将显示“曲线拟合过程”对话框。然后,单击“拟合”按钮开始迭代过程。如果成功,则将给出曲线拟合的精度(均方根)。值越小,表示越准确拟合所选的数据。如果失败,请在“参数”选项卡上更改初始猜测值,并再次尝试执行曲线拟合。 注: 曲线拟合使用各种最小二乘法拟合算法确定材料常数。例如,不同的数值技术和输入参数可能会导致不同的解。调整这些值可能导致会不同的曲线拟合。由于测试数据包括因不可控的因素而导致的变化,因此曲线拟合例程中的差异通常可以忽略不计。(有关曲线拟合方法的详细信息,请参考数值方法书籍或网站。)
“曲线拟合方案的结果”部分
此部分显示曲线拟合计算的材料模型常数。若要查看这些常数对数据拟合的影响,请更改一个值,并选择“显示的数据类型”以更新图形。
单击“确定”按钮关闭“曲线拟合材料数据”窗口时,这些值将从“曲线拟合材料数据”窗口复制到“单元材料定义”窗口。
以下方程用于各种材料模型:
- Neo-Hookean
- 单轴:Tu = 应力 = 2(λu - λu2)C10,其中,I1 = λu2 + 2λu-1
- 等双轴:TB = 应力 = 2(λB - λB-5)C10,其中,I1 = 2λB2 + λB-4
- 纯剪切:TS = 应力 = 2(λS - λS-3)C10,其中,I1 = λS2 + 1 + λS-2
- 体积:p = 压力 = -K(J-1),其中,J = λv3
其中,λ = 拉伸 = 1 + 应变
- Van der Waals:
- 单轴: 其中,I1 = λu2 + 2λu-1,I2 = λu-2 + 2λu
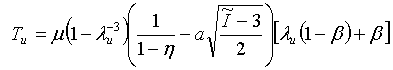
- 等双轴: 其中,I1 = 2λB2 + λB-4,I2 = 2λB-2 + λB4
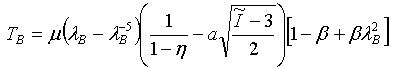
- 纯剪切: 其中,I1 = λS2 + 1 + λS-2,I2 = λS2 + 1 + λS-2
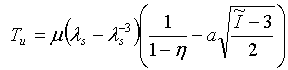
- 体积:p = 压力 = -0.5K(J-1/J),其中,J = λv3;其中,
- 单轴:
![]()
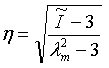
- Yeoh:
- 单轴: 其中,I1 = λu2 + 2λu-1
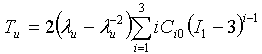
- 等双轴: 其中,I1 = 2λB2 + λB-4
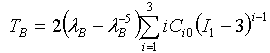
- 纯剪切: 其中,I1 = λS2 + 1 + λS-2
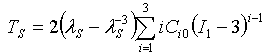
- 体积: 其中,J = λv3
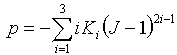
- 单轴:
“拟合曲线的输入数据比较”部分
此部分显示表格测试数据和拟合曲线。使用“显示的数据类型”下拉菜单选择图形中要显示的数据类型。输入的所有类型的数据均可显示,无论曲线拟合中是否使用该数据均是如此。当然,曲线拟合例程中未使用的数据不太可能具有非常拟合数据的常数。拟合曲线也可能不会很好地与表格数据吻合。
如果手动更改材料模型常数,则图形不会自动更新。若要更新图形,请重新选择“显示的数据类型”。
曲线拟合示例
下面,我们以 Ogden 材料模型为例,了解如何使用简单拉伸、等双轴和纯剪切测试数据。
- 将包含块体单元或二维单元的模型设置为非线性分析类型(“非线性材料模型静态应力”或“非线性材料模型 MES”)。测试数据以 MPa 为单位,因此模型单位应为牛顿和毫米。(1 MPa = 1 N/mm^2)
- 编辑单元定义。在部件的“单元定义”上单击鼠标右键,并选择“编辑单元定义”。将“材料模型”设置为“超弹性: Ogden”。单击“确定”。
- 编辑材料属性。在部件的“材料”上单击鼠标右键,并选择“编辑材料”。选择“[自定义]”,并单击“编辑属性”按钮。如果已知 Ogden 材料模型常数,则可直接输入。由于我们已有材料测试数据(如下),因此请单击“曲线拟合”按钮。
- 若要输入简单拉伸的应力-应变测试数据,请单击“简单拉伸”按钮。将行添加到电子表格并键入以下给定的数据,或将下面的文本复制并粘贴到文本文件(扩展名为 .CSV),并使用“导入”读取数据。完成后,单击“确定”。
- 采用类似的方式输入等双轴的应力-应变测试数据。单击“等双轴”按钮。将行添加到电子表格并键入以下给定的数据,或将下面的文本复制并粘贴到文本文件(扩展名为 .CSV),并使用“导入”读取数据。完成后,单击“确定”。
- 采用类似的方式输入纯剪切的应力-应变测试数据。单击“纯剪切”按钮。将行添加到电子表格并键入以下给定的数据,或将下面的文本复制并粘贴到文本文件(扩展名为 .CSV),并使用“导入”读取数据。完成后,单击“确定”。
- 在“控制”选项卡中,激活每个测试数据对应的复选框。
- 对于 Ogden 材料模型,“部分线性最小二乘法”的“曲线拟合方法”是一个很好的起点,因为它仅需一个参数的估计值(Alpha 值)。因此,请从下拉框菜单选择该方法。将其他设置保留为默认值。请注意,由于未输入体积数据,因此“体积模量阶次”将灰显。
- 在“参数”选项卡中,按如下所示设置“猜测的 Alpha”、“范围值”和“增量”。这将为要使用的解提供一个较为广泛的值范围,增量 20 是一个粗略值。但对于首次运行,它是一个很好的近似值,无需花太长时间即可计算所有数列。请注意,猜测值是 Ogden 材料模型的默认值。
阶次 猜测的 Alpha 范围值 增量 1 1.2 10 20 2 -2 10 20 3 6 10 20 - 在“控制”选项卡中,单击“执行曲线拟合”按钮,再单击“拟合”按钮。均方根误差为 0.184。与最大应力相比,它相对较大。单击“完成”按钮。
- 使用“显示的数据类型”下拉菜单,查看每个曲线拟合数据(简单拉伸、等双轴和纯剪切)的图形。曲线与测试数据非常合理地吻合(等双轴最吻合),因此找到的常数具有正确的数值阶次。
- 有了较好的估计值之后,请将“曲线拟合方法”切换为“Levenberg-Marquardt 算法”。然后使用先前得出的解,在“参数”选项卡中输入猜测值。由于估计值并不要求十分精确,因此使用以下舍入值便已足够:
阶次 猜测的 Mu 猜测的 Alpha 1 -0.16 6.2 2 4.4 0.5 3 0.026 9 - 在“控制”选项卡中,单击“执行曲线拟合”按钮,再单击“拟合”按钮。均方根误差为 0.183:与上一拟合相比几乎毫无改进。但请注意,此求解方法的速度比“部分线性最小二乘法”方法快得多。
- 您可使用不同的初始值执行其他试验,以找出备用最小值,但尝试阶次更高的模型似乎更高效。在“控制”选项卡中,将“模型阶次”设置为“5 阶”,并将曲线拟合方法设置为“部分线性最小二乘法”。然后,按如下所示在“参数”选项卡中输入猜测值。两点说明:首先,由于模型阶次已更改,因此在更有效的求解算法(如 Levenberg-Marquardt)中,使用先前的解找到的常数通常是无关的猜测值。在这种情况下,最好使用“部分线性最小二乘法”重新开始。其次,请注意,增量值相比之前有所降低。由于计算将涵盖一阶 Alpha 的每个组合、二阶 Alpha 的每个组合,以此类推,因此五阶求解将急剧生成大量计算结果!使用较小的增量值可以最大程度地减少曲线拟合例程所需的时间。
阶次 猜测的 Alpha 范围值 增量 1 1.2 10 10 2 -2 10 10 3 6 10 10 4 19 10 10 5 1 10 10 - 在“控制”选项卡中,单击“执行曲线拟合”按钮,再单击“拟合”按钮。均方根误差为 0.142。正如我们所预期的那样,“显示的数据类型”下的每条曲线均可更好地拟合测试数据。结果如图 1 中所示。您还可以执行其他试验,但考虑到测试数据的精度,此曲线拟合可以接受。
简单拉伸的测试数据
0,0
0.02,0.08
0.06,0.12
0.28,0.30
0.47,0.4
0.67,0.57
0.77,0.7
0.82,0.78
0.85, 0.9
0.89, 1.0
等双轴的测试数据
0,0
0.02,0.14
0.06,0.25
0.12,0.4
0.28,0.6
0.43,0.8
0.57,0.95
0.65,1.16
0.72,1.4
0.80,1.72
0.89,2.4
纯剪切的测试数据
0,0
0.02,0.08
0.07,0.2
0.20,0.37
0.59,0.71
0.73,0.92
0.83,1.1
0.89,1.28