三维 Drucker-Prager 材料模型用于建模地质材料,如土壤、粘土和岩石。此材料模型使用通过以下方程定义的屈服函数:
![]() (1)
(1)
其中:
![]() (2)
(2)
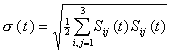 (3)
(3)
![]() (4)
(4)
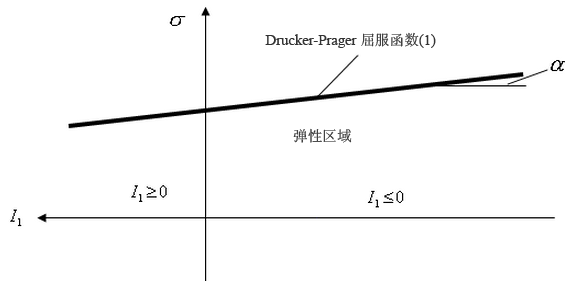
图 1:Drucker-Prager 屈服函数图
如果满足以下条件,则 Drucker-Prager 屈服标准将与 von Mises 完全塑性屈服标准相同:
 (5)
(5)
输入参数
参数 α 和 β 在“单元材料定义”对话框的“数据类型”选项卡上定义。如果在“输入数据的类型”下拉框中选择“模型常数”选项,则参数 α 和 β 将分别在 Alpha 和 Beta 字段中定义。如果在“输入数据的类型”下拉框中选择“土体力学系数”选项,则参数 α 和 β 将通过用于引用地质材料的常用参数计算。a 和 ß 将使用在“凝聚力”和“摩擦角”字段中输入的值通过以下方程计算:
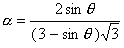 (6)
(6)
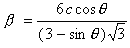 (7)
(7)
其中 ϑ 代表“摩擦角”字段中的值,c 代表“凝聚力”字段中的值。
修改 Drucker-Prager 屈服标准/屈服函数
Drucker-Prager 屈服标准未考虑两个地质材料属性。首先,大多数地质材料具有很少或没有任何抵抗拉伸载荷的能力。其次,地质材料的屈服表面和强度通常取决于压力载荷。修改 Drucker-Prager 材料模型将考虑这些属性。此模型包括三个部分,如图 2 所示。I1 大于张力截止 Tcut 的区域定义为张力截止区域。I1 小于封口屈服函数的区域定义为封口硬化区域。
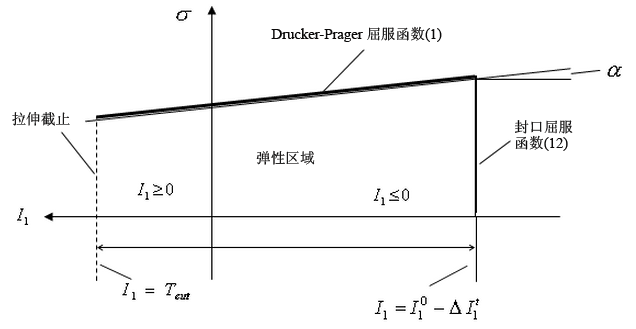
图 2:修改 Drucker-Prager 屈服函数图
张力截止区域
如果张力截止大于值 Tcut,则有三个选项可用于处理应力,同时又可保持迭代求解过程的稳定性。
1. 使用残差刚度 kres。该值的计算公式如下:
![]() (8)
(8)
其中 rres 是残差刚度系数,Ke 是原始弹性刚度。系数 rres 必须介于 0.0 和 1.0 之间。
2. 将三个法向应力设置为 Tcut 的三分之一,三个剪切应力设置为 0。
3. 将所有法向应力和剪切应力均设置为 0。
封口硬化区域
封口屈服函数定义为:
![]() (9)
(9)
其中 ![]() 是初始封口位置,
是初始封口位置,![]() 是压力硬化引起的封口位置的增量,
是压力硬化引起的封口位置的增量,
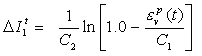 (10)
(10)
C1 和 C2 是两个封口硬化参数。这两个参数必须小于 0。![]() 是用于定义初始封口位置的用户输入系数。此系数必须小于或等于 0。
是用于定义初始封口位置的用户输入系数。此系数必须小于或等于 0。![]() 是塑性体积应变。
是塑性体积应变。
图 3 显示了不同封口函数系数的物理意义。在此图中,可以看出系数 C1 代表材料可能达到的最大塑性体积应变,C2 给出了对封口位置增加速率的测量。
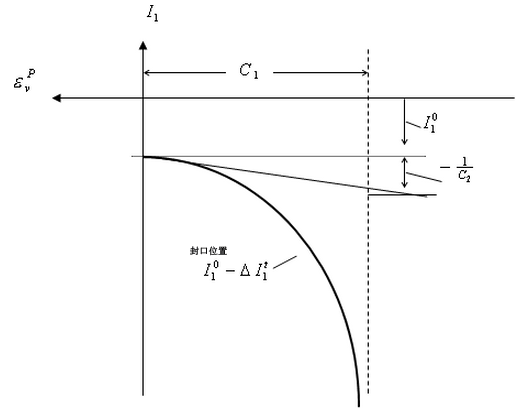
图 3:封口硬化曲线图
输入参数
张力截止区域
若要包括张力截止区域,必须在“单元材料定义”对话框的“张力截止”选项卡的“张力截止”下拉框中选择“包括”选项。值 Tcut 将在“张力截止系数”字段中定义。若要使用第一种方法处理大于 Tcut 的应力,请在“残差刚度系数”字段中输入 rres 值,然后在“拉伸截止后的应力”下拉框中选择“基于弹性刚度”。若要使用第二种方法,请在“拉伸截止后的应力”下拉框中选择“法向应力设置为平均值”。若要使用第三种方法,请在“拉伸截止后的应力”下拉框中选择“所有应力设置为 0”。
封口硬化区域
若要包括张力截止区域,必须在“单元材料定义”对话框的“封口硬化”选项卡的“封口硬化”下拉框中选择“包括”选项。在“第一个封口硬化常数”字段中输入值 C1。在“第二个封口硬化常数”字段中输入值 C2。在“初始封口位置”字段中输入值 ![]() 。
。