临界屈曲载荷

临界屈曲载荷分析（也称为特征值屈曲分析）可检查模型在主要轴向载荷下的几何稳定性。在大多数产品的正常使用过程中，如果发生屈曲，则可能造成灾难性的后果。几何体开始变形后，其甚至无法再承受最初施加的力的一小部分。

适用于临界屈曲的单元类型包括梁、板和块体（及其变型）。所选的单元会影响计算得出的屈曲乘子类型。例如，从数学角度来说，梁单元仅表示为具有横截面的直线，梁仅可计算全局屈曲。板和块体单元可以计算局部屈曲，因其横截面通过单元建模。请参见图 1。

(a) 梁单元将提供全局屈曲形状和载荷乘子。

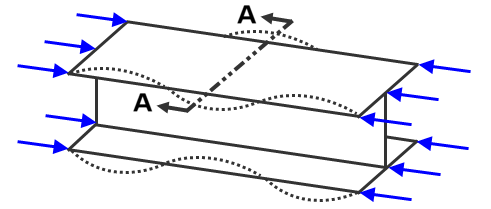
(b) 板和块体单元可提供全局和局部效果。在此示例中，梁的法兰局部屈曲，可能处于小于导致全局屈曲的载荷的临界载荷作用下。

图 1：柱或杆上的偏心载荷

由于临界屈曲通过求解特征值问题（如模态分析）进行计算，因此其结果适用于薄型和细长结构（如 Euler 柱）。不包含针对短柱、厚板（相对于板的长度和宽度而言）或材料的屈服强度的修正。请参见图 2。此外，其为线性分析。不存在变形引起的刚度变化，因而不存在大变形效果，例如 P-delta（载荷-变形）效果。因此，可以确定临界载荷和屈曲振型，但无法提供屈曲后发生的情况。（如果需要屈曲后的结果，请执行非线性分析。）

临界载荷

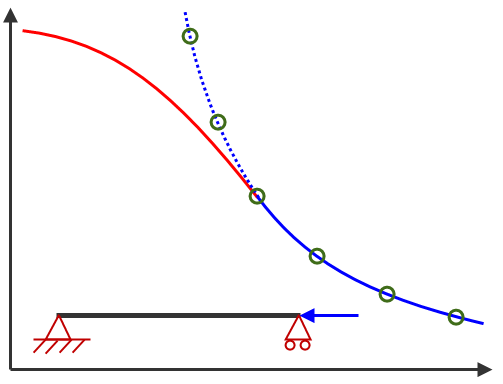
长细比

图 2：柱或杆上的偏心载荷

（ Euler 方程， Johnson 修正，计算得出的结果）

使用屈曲分析可确定指定的一组载荷是否会造成屈曲和获取屈曲的振型。然后，可以设计支架或加强构件以防止局部屈曲。当部件或装配件受到轴向载荷的作用或当模型遭受边缘压缩时，该分析非常有用。

不导致压缩的载荷不会影响屈曲计算。请务必注意，计算梁单元的临界屈曲载荷时，将仅考虑载荷的轴向分量。例如，假设在杆端部施加一个偏移载荷（请参见图 3(a)）。该载荷可以表示为梁模型端部上的轴向载荷和力矩（图 3(b)）。由于力矩不会在梁单元上创建轴向应力，因此此分析中的偏移载荷产生的结果与纯轴向载荷相同。（力矩会创建弯曲应力；梁单元一侧上的理论压缩不会影响屈曲计算。）

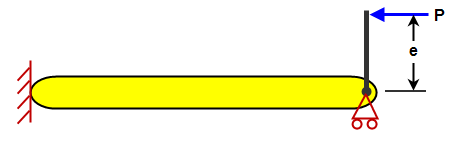
(a) 杆的物理模型，载荷 P 偏离中心线的距离为 e。

(b) 在 FEA 中创建的梁模型。载荷偏心距会产生施加到该节点的力矩。由于梁单元和临界屈曲的性质，该力矩不会影响结果。此示例中使用了错误的单元类型。

图 3：柱或杆上的偏心载荷

计算得出的屈曲载荷乘子将显示在“结果”环境、日志文件和摘要文件中。屈曲载荷乘子指示模型发生屈曲的时间。将在模型上施加的所有载荷乘以屈曲载荷乘子，即得到导致屈曲的理论载荷。由于实际制造过程中产生的缺陷（初始曲率、施加的偏心载荷等），真实部件容易在低于理论值的载荷下发生屈曲。这些小偏差可能会对现实中的临界载荷产生巨大影响。

如果屈曲载荷乘子为负值，则表示反转外施载荷（并通过乘子缩放）将导致模型屈曲。例如，将 1000 PA 的压力施加到模型上，但该压力导致模型处于拉伸状态。屈曲乘子 -0.75 指明部件将在 750-Pa 的压缩载荷作用下发生屈曲。

包括恒定载荷

临界屈曲会通过计算得出的屈曲乘子缩放所有外施载荷。在某些情况下，用户可能想要缩放活载荷（如压力），而不想缩放其他载荷（如重力）。如果恒定载荷很重要且必须包括在内，请使用以下步骤。

通过经验、执行手动计算或运行分析估算屈曲乘子。称其为最后一个屈曲乘子。
将恒定载荷更改为“恒定载荷/最后一个屈曲乘子”的值，保留活荷载的额定值。
运行屈曲分析。
如果新屈曲计算的结果给出相同的屈曲乘子，则该解适用。屈曲结果中的恒定载荷为（恒定载荷/最后一个屈曲乘子）*（新屈曲乘子)= 恒定载荷，导致屈曲的可变荷载为（可变荷载）*（新屈曲乘子）。
如果新屈曲计算的结果给出不同的屈曲乘子，请将最后一个屈曲乘子替换为新值。重复步骤 2 到 5。

由于临界屈曲是特征值解，因此位移结果将显示屈曲振型。位移的数值没有意义。同样，临界屈曲分析中不存在应力或应变结果。