von Mises 材料模型可用于二维、梁、壳、块体和四面体单元。这些材料模型适用于弹性材料要承受的载荷超过其屈服强度的情况。这种情况下,材料将发生塑性变形。von Mises 双线性强化材料模型将使用双线性曲线计算应力值。应力与应变弹性区域的坡度等于弹性模量,应力与应变塑性区域的坡度等于应变硬化模量。
可使用两种类型的强化材料模型。各向同性强化模型涉及均匀地屈服整个屈服面。随动强化涉及屈服面的移位(主要因载荷变化引起)。请参见图 1 和 2。如果分析涉及循环载荷(包辛格效应),则首选随动强化模型,但应根据实际材料的应力-应变行为来确定是选择各向同性还是随动强化。
|
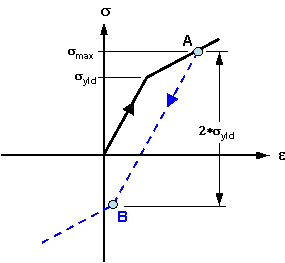
单轴应力-应变曲线。如果部件变力超出屈服应力,它将开始塑性变形。如果转到最大应力(点 A)并释放载荷,它将沿虚线卸载。如果重新加载该部件,则在应力到达点 A 前不会发生其他塑性变形。 如果将部件置于压缩,它将沿虚线进行弹性压缩,直至到达点 B,然后将在压缩中屈服。 对于各向同性强化,从点 A 到点 B 的应力变化为获取的最大应力的两倍。 |
|
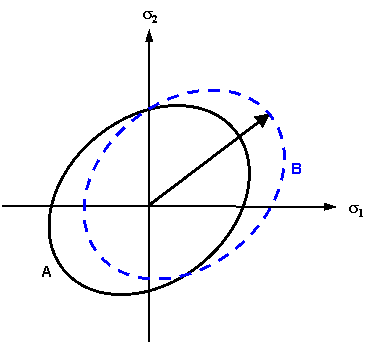
双轴应力-应变曲线。在双轴情况下,初始屈服面(表面 A)内的任意应力组合都是在弹性区域。一旦部件超出初始屈服面,该部件将出现塑性变形。 对于各向同性强化,屈服面的中心保持固定,但表面的大小将增加。新屈服面(表面 B)内的任何应力状态将出现弹性变形,当应力状态到达表面 B 时将发生新塑性变形。 |
| 图 1:各向同性强化 |
|
单轴应力-应变曲线。如果部件变力超出屈服应力,它将开始塑性变形。如果转到最大应力(点 A)并释放载荷,它将沿虚线卸载。如果重新加载该部件,则在应力到达点 A 前不会发生其他塑性变形。 如果将部件置于压缩,它将沿虚线进行弹性压缩,直至到达点 B,然后将在压缩中屈服。 对于随动强化,从点 A 到点 B 的应力变化为屈服应力的两倍。 |
|
双轴应力-应变曲线。在双轴情况下,初始屈服面(表面 A)内的任意应力组合都是在弹性区域。一旦部件超出初始屈服面,该部件将出现塑性变形。 对于随动强化,屈服面的中心会移动,但表面的大小将保持不变。新屈服面(表面 B)内的任何应力状态将出现弹性变形,当应力状态到达表面 B 时将发生新塑性变形。 |
| 图 2:随动强化 |
下面列出了 von Mises 材料属性。两种模型的 von Mises 材料属性相同。不过除此以外,可能还需要定义一些各向同性材料属性。
屈服强度
材料屈服强度是指应力与应变曲线上材料最初开始转到塑性应变的点。屈服一次后,新屈服应力取决于强化类型和载荷历史。
应变硬化模量
应变硬化模量是指材料屈服点之后的应力与应变曲线坡度。
从材料库加载部件的材料属性时,应变硬化模量主要取决于定义双线性应力-应变曲线的三个点,即 (0,0)、屈服点以及库管理器中采用极限强度与 2 英寸处的延伸度进行标识的点。然后,按如下所示计算应变硬化模量:

应变硬化模量 = [极限强度 - 屈服强度]/[(2 英寸处的延伸度)/100 - 屈服应变]
其中屈服应变为与屈服强度对应的应变,或屈服应变 = (屈服强度)/(弹性模量)。极限强度、屈服强度、2 英寸处的延伸度和弹性模量存储在材料库中。
结构不稳定性
使用 von Mises 材料模型时,如果超出材料屈服强度,结构的刚度会减小,且结构可能会变得不稳定。在这种情况下,相比所有应力均在弹性范围内时,结构承受应用的载荷的能力会显著降低。这种不稳定性证明其本身属于复杂的数值求解收敛、不稳定或异常的应力结果等。这种情况下,对于模型设置进行以下调整非常具有帮助:
- 使用规定位移替换力载荷。
- 在不稳定周期使用较小的时间步大小,使用多个时间间隔分析事件。
- 尝试执行 MES Riks 法分析,该分析用于捕获后屈曲现象。有关其他信息,请参见以下两个帮助主题:
- MES - 非线性结构页面中的 MES Riks 法分析内容
- 分析参数:MES Riks - 后屈曲页面。