运动仿真的理论基础

运动仿真是指在虚拟实验室模拟物理运动的工程设计。使用运动仿真执行工程分析时，需采用与传统应力分析不同的视点。

根据工程培训知识，我们已得知应力是力的函数，即 σ= f(力)。变形或位移是力的另一个函数，即 d = g(力)。而在运动仿真中，我们假定设计力通常是不确定的，它是由某种操作或运动产生的。在这种情况下，力和应力为位移或变形的函数，即力 = f(d) 且 σ = g(d)。变形或位移由物理控制方程直接计算得出。

对比机械运动仿真与传统方法

我们将以简单的悬臂梁为例，对比传统应力分析与运动仿真之间的差异。

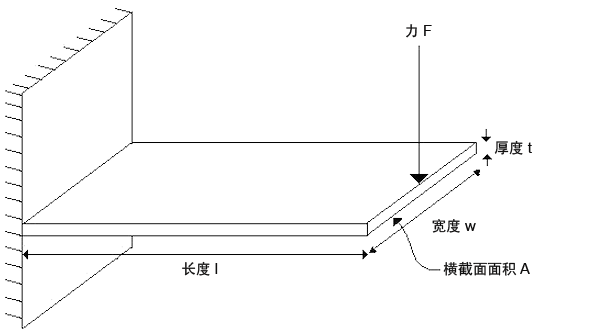
工程设计手册指出，若悬臂梁受力于固定端 (A) 相对端的力，则最大应力（A 端）的计算公式为：

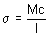
[1]

其中，M 为力 F 产生的力矩 (M = Fl)，c 是中性轴到梁边的距离 (c = t/2)，而 I 是面积惯性矩 (I = wt ³ /12)。此结果是结合胡克定律 (|F| = k|d|) 并在考虑悬臂梁弯曲度的基础上计算得出的。胡克定律认为，力是位移的线性函数。该观点奠定了传统应力分析的基础，同时也是现代有限元应力分析的基础。

在有限元分析中，矩阵方程 {F} = [K]{d} 利用力矢量 {F} 和刚度矩阵 [K] 求解位移矢量 {d}。随后，根据方程 {σ} = E{ε} 计算得出应力，其中 {ε} 是应变矢量，即标准化位移矢量。E 是弹性模量，对应于胡克定律常数 k。

仅当悬臂梁处于静止状态时方程 [1] 才成立，进而才能顺利求解。而在实际机械工程设计中，绝不会考虑静止状态。设计必须考虑最糟糕的情况，即悬臂梁发生移动或受力时，而这时的应力要大于静止条件下的应力。

这正是运动仿真用于完善设计流程之处。您可以对整个运动仿真，而不仅仅是获得静态求解。运动仿真还有一项额外的优势，即计算和考虑运动所产生的力。根据牛顿第二定律

F = ma

[2]

即：力等于质量乘以加速度。而质量是物质的固有特性，加速度是速度变化的速率。该定律限定，质量是阻碍运动变化的一项物质特性。请注意，在重力的影响下，静止物体会因自身质量 m 产生一个力 mg，其中，g 为重力加速度。在加速度恒定（重力场靠近地球表面）或瞬时运动（如长度为 Δt）等特殊情况下，方程 [2] 可改写为：

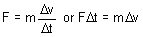
[3]

其中，Δv 是速度在 Δt 时间内的变化量。1,000,000 lb 的力在 0.000001 秒内产生的冲量（或动量改变量）与 1 lb 力在 1 秒内产生的冲量相同。

运动仿真需要结合使用牛顿第二定律与胡克定律，具体如下：

F = ma = -kd，或 ma + kd = 0

[4]

由于力与位移方向相反，因此 k 前有一个负号。另外注意，大小模糊的力是可以被抵消的，且时间的概念已通过术语“加速度”引入。若要模拟真实世界的问题，还必须考虑阻尼或摩擦。这些耗散力的计算公式为

F = -cv

[5]

其中 v 是速度，c 是常数；注意耗散力是如何阻碍运动的。合并方程 [4] 和 [5] 之后，即可得出：

ma + cv + kd = 0

[6]

或以矩阵形式表示：

[M]{a} + [C]{v} + [K]{d} = 0

[7]

它是虚拟工程的基本方程。注意它是如何结合运动、阻尼和机械变形进行建模的。若仍需要了解应力，则在分析期间可随时利用公式 {σ} = E{ε} 进行计算。其中，公式中的 {ε}（应变矢量）可利用位移矢量 {d} 轻松算出。虚拟工程为“最糟糕的情况”提供了一种设计方式。即便以简单的悬臂梁为例，方程 [7] 的求解也优于人工计算结果。但是，随着计算机技术的进步，即便更复杂的问题，也可以轻松求解。

数值示例

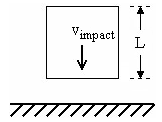
我们通过数值示例展示虚拟工程的强大功能。假定质量为 m 的立方体沿一个面碰撞一个刚体曲面。我们要了解该立方体发生的最大变形量。首先，我们对最大压缩长度进行人工计算。然后使用虚拟工程求解同一问题并对两种结果进行比较。

发生接触前的立方体。

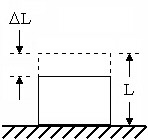
发生最大变形时的立方体。

根据牛顿第二定律，冲击力通过方程 [1] 计算得出。根据传统物理学原则，我们假定立方体的所有质量均位于形心。若同时假定立方体上任意特定位置的加速度在整个碰撞过程中均为常数，则方程 [1] 为：

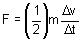
[8]

其中，Δv 是立方体顶部速度在碰撞间隔 Δt 内的变化。由于我们针对形心应用方程 [1]，因此方程 [8] 中需要使用系数 1/2，即立方体中间面的加速度需为顶面的一半。换言之，即一旦接触，我们认为立方体顶部的移动速度是形心速度的两倍。在假定加速度恒定的基础上，我们利用基本运动学原理可以获得立方体在碰撞期间变形量的表达式：

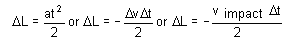
[9]

其中，v _碰撞 是立方体（因此也是其顶面）在接触时的速度。由于 Δv 为负值而 ΔL 需为正值，因此，方程 [9] 中需要一个负号。注意 Δv 是如何替换为 v _碰撞 的（替换的原因是，在发生最大变形时立方体的顶部不移动）。

根据胡克定律，立方体上力的计算方程为：

[F = -kDL]

[10]

将方程 [8]-[10] 合并在一起，即可得出：

[11]

将 k 转换成 E 的对应形式（对于长度为 L，变形轴垂直于特定表面的立方体来说，k = EL），我们将得到：

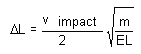
[12]

使用该软件，我们可以模拟相同的碰撞问题。首先构建一个长度 (L) 为 1.0 英寸、质量 (m) 为 0.000253 lbm 的立方体模型。该立方体材料的弹性模量 E 为 10⁷lb/in²。仿真运动是该立方体从 100 英寸的高度落下。它将产生 278 英寸/秒的冲击速度（v _碰撞）（当重力场的强度为 386.4 英寸/秒² 时）。该软件预计最大变形 (ΔL) 为 0.000694 英寸，十分接近方程 [6] 计算得出的值 0.000699。

本示例足以说明在不使用数字原型设计软件的情况下分析简单碰撞问题的难度，因此，对于更错综复杂的几何体进行手动计算时，其难度可想而知，有时甚至根本不可能实现。您可以采用传统的有限元分析 (FEA) 方法。然而，此类分析会忽略（大）运动，因此只有在了解冲击力的前提下方可适用。此类分析的不足之处主要体现在，它会忽略在实际碰撞中因力的波动而产生的振动。

力的估算方法

有三种常用方法用于估算传统 FEA 中使用的力值：经验法、刚体动力学分析法以及物理实验法。

• 经验法

  某些工程师凭借之前处理相似问题的经验来估算这些力。通常，他们会根据特定的安全系数来估算，这些安全系数既要足以阻止故障，又不能过于保守从而导致产生过度设计的部件。

• 刚体动力学分析法

  刚体动力学程序使用部件模型来计算运动产生的力。为获得这些力的数值，此类程序会使用模糊定义的刚度。鉴于这些程序受限于刚体假设条件，使用这些刚度计算所得的力通常是不准确的。

• 实验法

  对零件原型进行实验是一种获得力值的精确方法。但此方法完全不如计算机分析方法经济实用。

结论

利用事件仿真，用户能够采用最少的假设完成整个物理事件的建模。尤其是，用户不必假设静止条件或估算运动产生的力值。另外，运动仿真还具备一项有利的附加优势，即生成运动的逐帧记录，而非仅在结束时生成一个快照。