损伤理论描述

概述：

损伤模型可模拟弹脆性正交各向异性材料（例如，复合材料）的损伤出现和渐进增长情况。该模型主要用于模拟纤维增强复合材料。损伤模型描述了以下三个材料响应阶段：

1. 未损坏的材料响应（必须是线性弹性响应）
2. 损伤萌生
3. 渐进损伤增长。

在该模型中，材料损伤的特点是材料刚度降级。假设复合材料的纤维平行，且位于单元材料轴 1 方向上。考虑以下四种不同的失效模式：

• 纤维在拉伸作用下断裂；
• 纤维在压缩作用下屈曲和纽结；
• 矩阵在横向拉伸和剪切作用下开裂；
• 矩阵在横向压缩和剪切作用下破碎。

材料特性定义为 σ = C_dε，其中，C_d 是反映损伤的弹性矩阵，其计算公式如下：

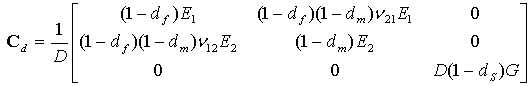
其中

• D=1-(1-d_f)(1-dm)ν₂₁ν₁₂ν
• d_f 表示纤维破坏
• d_m 表示基体破坏
• d_s 表示剪切破坏
• E₁ 是纤维方向上的杨氏模量
• E₂ 是纤维垂直方向上的杨氏模量
• G 是剪切模量
• ν₂₁ 和 ν₁₂ 是泊松比。

损伤萌生：

损伤萌生准则考虑到了四种不同的损伤模式，具体形式如下：

模式 I：纤维拉伸 ( >= 0)
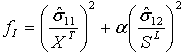
模式 II：纤维压缩 ( < 0)
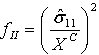
模式 III：矩阵拉伸 ( >= 0)
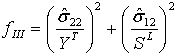
模式 IV：矩阵压缩 ( < 0)

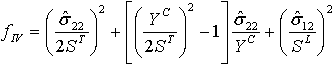
其中

• f_I、f_II、f_III、f_IV 是与损伤萌生准则关联的变量。值大于等于 1.0 表示符合萌生准则。
• X^T 表示纵向拉伸强度
• X^C 表示纵向压缩强度
• Y^T 表示横向拉伸强度
• Y^C 表示横向压缩强度
• S^L 表示纵向剪切强度
• S^T 表示横向剪切强度
• α 表示确定剪切应力对纤维拉伸萌生准则有何影响的系数，并且 0<= α <= 1。

、 和 是有效拉伸应力 的分量，其计算公式为 =Mσ。σ 是公称应力，M 是损伤运算符，其定义如下：

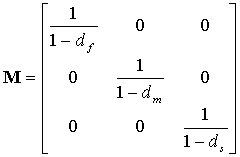
内部损伤变量 d_f、d_m 和 d_s 由对应于上述四种模式的损伤变量 d_ft、d_fc、d_mt 和 d_mc 衍生而来：

d_f = …

• d_ft（如果 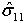>= 0）
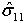• d_fc（如果 < 0）

d_m = …

• d_mt（如果 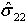>= 0）
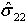• d_mc（如果 < 0）

d_s = 1-(1-d_ft)(1-d_fc)(1-d_mt)(1-d_mc)

下面给出了损伤变量 d_ft、d_fc、d_mt 和 d_mc 的方程。

损伤演变：

下面，我们将根据上一部分中的损伤萌生，为每种模式定义损伤变量的演变情况。为了缓解材料软化过程中的网格从属关系，我们引入了等效应力和位移。

为以下四种损伤模式定义等效应力和位移：

• 纤维拉伸模式：

  

  

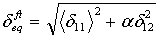
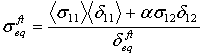
• 纤维压缩模式：

  

  

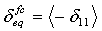
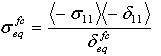
• 矩阵拉伸模式：

  

  

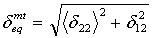
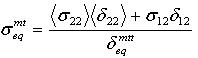
• 矩阵压缩模式：

  

  

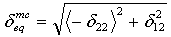
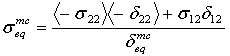
其中，δ_ij = L_cε_ij，特征长度 L_c 计算为积分点面积的平方根。运算符 <x> 是 Macauley 换位运算符，定义为 <x> = (x + |x|)/2。

根据等效应力和位移，损伤变量的计算公式如下：

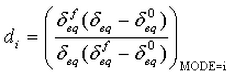
其中，i 对应于 I 到 IV 这四种模式（或 d_ft、d_fc、d_mt 和 d_mc）。结果介于 0 到 1 之间，其中，0 表示无损伤且单元可承受满载，1 表示全损且单元在各个方向上都无法承受任何载荷。

δ⁰_eq 和 σ⁰_eq 是符合萌生准则的初始等效位移和应力。其定义如下

.

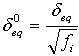
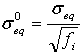δ^f_eq = 2G^c_i/σ⁰_eq 是此失效模式中材料全损时的等效位移，其中，在失效模式 i（拉伸或压缩）作用下的耗能 G^c_i 可控制损伤演变。

每个损伤定律的最大有限元大小为 L_c <= 2 * E_iG^c_i/(X_i)²，其中，Eⁱ、G^c_i 和 Xⁱ 分别是杨氏模量、断裂能和强度。同样地，i 对应于 I 到 IV 这四种损伤模式（或对应名称，具体取决于变量）。

损伤稳定性和粘性正规化：

为了解决隐式分析中由于材料软化行为和刚度降级而引起的收敛问题，我们引入了广义 Duvaut-Lions 粘性正规化方案。在正规化方案中，粘性损伤变量的定义如下

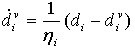
η_i 是代表粘性体系松弛时间的粘性系数，d_i 是在非黏性支柱模型中算出的损伤变量，其中，i 表示损伤模式（I 到 IV，或与变量一致的 ft、fc、mt 和 mc）。正规化的损伤变量将更新为：

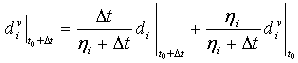
粘性材料的损伤响应表示为 σ = C_d(dν)ε。粘度参数较小通常有助于提高软化方案中的模型收敛速度，而不会影响结果。

其他：所需的其他计算方法如下所示：

• 互补的自由能密度：

  

• 破坏能量：

  

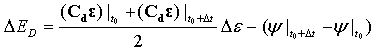
粘性能量耗散：

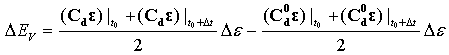
参考文献：

1. Hashin, Z., A fatigue failure criterion for fiber reinforced materials, Journal of Composite Materials, 7 (1973), 448-464.
2. Lapczyk, I. 和 Hurtado, J.A., Progressive damage modeling in fiber-reinforced materials, Composites: Part A, 38 (2007), 2333-2341.
3. Iannucci, L. 和 Ankersen, J., An energy based damage model for thin laminated composites, Composites Science and Technology, 66 (2006), 934-951.
4. Maimi, P., Camanho, P.P., Mayugo, J.A., 和 Davila, C.G., A continuum damage model for composite laminates: Part I - constitutive model, Mechanics of Materials, 39 (2007), 897-908.
5. Maimi, P., Camanho, P.P., Mayugo, J.A., 和 Davila, C.G., A continuum damage model for composite laminates: Part II - computational implementation and validation, Mechanics of Materials, 39 (2007), 909-919.