非线性稳态热传递分析

过程概述

当传导系数与温度成函数关系（正交各向异性材料模型）或当将辐射应用于模型时，必须执行多个迭代才能求解稳态热传递分析问题。例如，如果温度未知，则无法得知热传导率，而没有热传导率便无法计算温度。因此，需要使用迭代方法。

除了直接使用温度相关的传导率和辐射之外，还使用这些效应来计算体对体辐射和对流与温度的函数关系，如以下部分所述。

在稳态求解器的每个迭代中，温度相关的传导系数和辐射热传导率将根据之前的节点温度估值 (T i cur) 进行估计。在第一次迭代中，初始温度将通过单独（在节点上单击鼠标右键，然后选择“添加：温度”命令）或整体（“分析参数”屏幕中“选项”选项卡的“默认节点温度”）应用于节点的值给出。在“FEA 编辑器”环境中指定节点的初始温度值后，这些值将替代默认值。然后，对模型进行分析。生成的温度 (Ti new ) 将与之前的节点温度估值进行比较。如果之前的温度和生成的温度之间的差值可接受（如下定义），则分析迭代将停止。如果差值不可接受，则将根据假设的新节点温度估值重新计算热传导率和辐射热流率，再次求解该问题。图 1 显示了此过程。

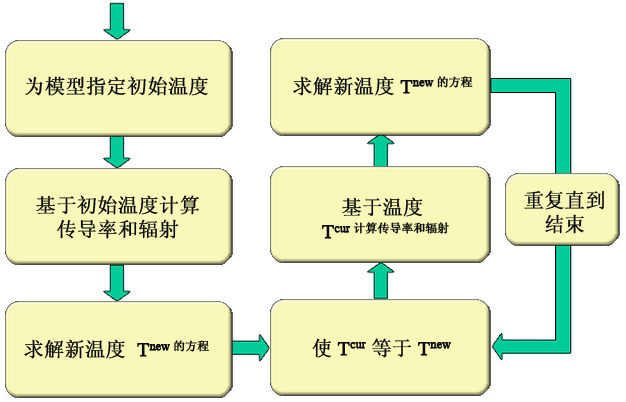
图 1：非线性求解过程

实际上，用于计算下一次迭代中的传导率或辐射的温度 (T cur ) 将通过 [(1-A)(T i old )+(A)(T i new )] 计算或等于 [T i old +A(T i new -T i old )]，其中 A 为松弛参数（在“分析参数”屏幕中“高级”选项卡的“松弛参数”字段中定义），T i old 为上一次迭代中计算得出的温度。通常建议使用的 A 值为 1。下一次迭代的假定温度为通过刚刚执行的迭代生成的温度 (T i new )。如果需要以较小值更新温度 T cur 以抑制可能的迭代过度振动，则使用介于 0 和 1 之间的值。由于值 0 会导致温度不更新，因此请使用非零的松弛参数。如果节点温度在连续迭代之间循环而不是平滑收敛，则需要不等于 1 的松弛参数。

使用假定的新温度更新传导系数并重新计算辐射方程，重复执行该过程。

传导与温度的函数关系

如果使用正交各向异性材料模型，则可以指定传导与温度的函数关系。需要提供一组与传导值对应的温度值。必须以温度升高的顺序提供正交各向异性属性。求解中遇到的温度范围不得超过材料属性适用的温度上限和下限。通过在提供的温度值之间进行线性插值计算传导系数。

初始温度的默认值为 0。如果不变，则为确定传导系数而指定的最低温度必须小于或等于 0。初始温度用于计算初始传导系数。之前介绍的非线性选项必须用于迭代温度以更新传导系数。

辐射

通过受到辐射的表面的热通量（热传递/时间/面积）可由以下方程表示：

其中

辐射参数 F rad 和 Trad 是基于表面的载荷，将在“表面属性”屏幕的“辐射”选项卡上指定。模型温度可以通过 °F 或 °C 的形式输入。可通过“分析参数”屏幕中“辐射”选项卡上的输入将它们转换为绝对温度。Stefan-Boltzmann 常数也在此屏幕上指定。

分量 (T s 4 -T rad 4 ) 可以改写为 (T s 2 +T rad 2 )(T s +T rad )(T s -T rad )。如果假设分量 (T s 2 +T rad 2 )(T s +T rad ) 为常数，则可使用线性求解算法。非线性运行时间选项用 T i old 代替方程恒定部分中的 Ts 并如上所述进行迭代。如果解在迭代过程中发生振动，则可能需要减小松弛参数 (A)。

体对体辐射

之前讨论的辐射类型适用于向周围环境发出辐射的部件。在实际应用中，通常适用于那些通过辐射与同一部件和其他部件上的其他表面进行热传递的部件。在显示区域中单击鼠标右键，然后选择“体对体辐射”命令或选择“设置”“热载荷”“体对体辐射”。可以将彼此之间通过辐射进行热传递的表面放入单独的壳体。可以将这些表面的辐射率定义为恒定值或温度相关值。有关更多详细信息，请参见体对体辐射。

在某些情况下，可以使用温度相关的传导仿真体对体辐射，如下图所示：

图 2：体对体辐射

若要使此近似法准确，需要满足以下要求：

  1. 主体之间的视角系数必须接近 1。
  2. 流出系统的热通量忽略不计；即热量没有辐射到环境中。
  3. 每个主体的表面面积都相等。
  4. 通过手动计算、试验或之前的分析（多次迭代）已获知表面的预期温度。

如果两个主体互相面对且中间无阻碍，则可以根据主体的表面热阻和空间热阻将它们之间交换的热量写作：

其中 T A 和 T B 是表面 A 和 B 的温度（绝对温度），ε A 和 ε B 是表面 A 和 B 的辐射率，VF AB 是两个表面之间的视角系数。

两个主体之间通过传导实现的热流量为：

由于辐射的热流量必须等于传导的热流量，因此令上述两个方程相等并将 如下展开：

从而得出：

即使用绝对温度的解。

在两个主体之间的新部件中构建一个单元层。将“材料模型”设置为“正交各向异性”，以便材料属性与温度相关。使用上述方程通过预估的表面温度 T A 和 T B （采用绝对温度）计算传导率。将计算得出的传导率输入温度 Taverage = 0.5(T A +T B )（按照“单位定义”对话框中的设置，采用绝对温度或温度）下的材料属性中。通过估算 T A 和 T B 其他值的 T average 和 K，输入其他数据点。请确保在材料属性中包括一系列的温度 T average ，以便计算得出的温度不超出材料属性的范围。

注：
  • 对于体对体辐射近似法，在跨距 L 内仅使用一个单元。不得使用 L 方向的网格。
  • T A 和 T B 的不同组合可以产生不同的传导率 K。对于相同的温度 T average ，要输入的 K 应为给定温度 T average 产生的所有传导率平均值。

热载荷与温度的函数关系

在稳态热传递分析期间，对流和热生成载荷可能随温度变化。若要应用温度相关的对流载荷，请转到“表面属性”屏幕并激活“对流”选项卡的“温度相关的对流系数”复选框。然后，可以定义对流系数与温度曲线，用于控制对流造成的通过该表面的热流量。若要应用温度相关的热生成载荷，请转到“单元定义”并激活“载荷”选项卡的“温度相关”复选框。然后，可以定义一个热生成速率与温度曲线，用于控制通过此部件的热生成。

父主题： 稳态热传递