在“FEA 编辑器”或“结果”环境中使用“分析” “分析”
“分析”  “优化”可访问“设计优化”对话框。“参数”选项卡只用于指定“设计优化”的求解参数;此选项卡上的值不会影响设计分析。
“优化”可访问“设计优化”对话框。“参数”选项卡只用于指定“设计优化”的求解参数;此选项卡上的值不会影响设计分析。
“优化方法”设置设计优化要使用的算法。选项如下所示:
- SLP:使用序列线性规划法求解分析。首先,创建目标和约束函数的泰勒级数近似(线性)。此近似可用于求得最优解。此方法是最可靠的求解方法。
- SQP:使用序列二次规划法求解分析。首先,创建目标函数的泰勒级数近似(二次曲线)。然后,创建约束函数的线性近似。这些近似可用于求得最优解。此方法的速度比 SLP 快,但并不是很稳定。
- 响应面:创建全局函数,表示模型对不断更改的设计变量做出的响应。由于该函数涵盖的跨度较大,因此不如 SLP 或 SQP 方法那样详细。所以,使用“响应面”法找到的最优化值可能只是实际优化值的近似值。若要提高解的精确性,请运行“响应面”以接近优化值。然后,使用 SLP 或 SQP 方法并根据响应面结果输入相应内容。
请注意,仅当目标在每个设计变量的下限到上限设计范围内为凸面(求解最小值时)或凹面(求解最大值时)时,才能保证存在绝对最优解。如果优化曲线发生屈折变化,则有可能会求得局部最佳结果;如果使用不同的优化方法或调整上限和下限,则有可能会求得不同的最佳结果。请参见图 1 中所示的示例。
|
目标/约束 设计范围 (a) 目标/约束方程的理论曲线。如果该曲线已知,则最小值显而易见,但我们事先并不知道该曲线。数值方法将计算该曲线,并尝试以最简便的计算方式找出最小值。 |
 (b) 使用 SLP 方法,可以通过设计范围的上限和下限计算出曲线。由于下限是最小值,因此线性搜索将从下限开始。 |
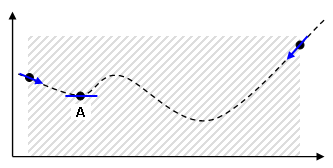 (c) 使用各种参数,搜索例程在理论曲线的 A 点处求得最小值。一旦找到最小值,即表示该解已收敛。它并非绝对最小值,而是局部最小值。 |
 (d) 使用 SQP 方法,利用二次方程估算理论曲线。 |
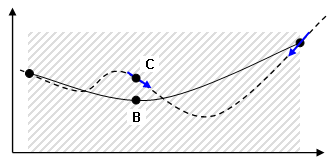 (e) 二次方程的最小值出现在 B 处。在设计变量的此值处,理论曲线位于 C 处且计算出了斜率。 |
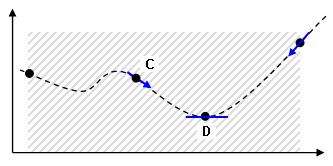 (f) 搜索例程使用各种参数在理论曲线的 D 点处求得最小值。一旦找到最小值,即表示该解已收敛。 |
| 图 1:求最小值的例证 |
对于图 1,还有几点值得注意。
- 与使用 SQP 方法相比,在使用 SLP 方法时,搜索方向和移动限制更容易受上限和下限的影响。
- 通过上述方法求得的最优值并不能保证符合约束(应力、变形等的上限和下限)。找到斜率为 0 的点(最优点)后,如果违反约束,例程将无法确定要移动到哪个位置。在这种情况下,可以调整已违反的设计变量范围并重复优化分析。
“最大迭代次数”字段指出优化过程中要使用的迭代次数。如果在此迭代次数内未求得解,则设计优化将停止。完成分析后,请始终检查日志文件,了解约束与指定限制之间的接近程度。
请记住,完整优化分析运行分析的次数可能是指定的最大迭代次数的好几倍。如果常规分析需要半小时完成,且您指定 20 次迭代,则整体优化可能至少需要 10 小时才能完成,甚至有可能长达 60 至 100 小时才能完成(具体取决于设计变量数以及收敛所需的迭代次数)。
“最大目标更改”字段确定解何时收敛到该答案。它是容差。如果每个约束值(在“性能”选项卡上指定的目标/约束)在不同迭代之间发生的更改位于当前结果乘以该容差所得出的范围内,则表示解已收敛。(从数学角度来说,-容差 <= (当前结果 - 上一个结果)/当前结果 <= +容差。)
 设计变量
设计变量