Duncan-Chang 理论描述

Duncan-Chang 材料模型用于模拟土体。它假设存在应力/应变双曲线关系，并根据三轴土体测试而构建。原始模型假定泊松比为常数（由 Duncan 和 Chang 于 1970 年提出），而修订后的模型则认为，泊松比因应力相关泊松比（E-v 模型，由 Kulhawy 和 Duncan 于 1972 年提出）或应力相关体积模量（E-B 模型，由 Duncan et al 于 1980 年提出）而异。

公式：

根据标准的三轴土体测试，该模型通过以下双曲线关系近似描绘应力-应变：

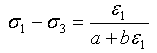     (1)

其中，σ1 和 σ3 是最大主应力和最小主应力；ε1 是最大主应变（轴向应变）。在此需要指出的是，我们遵循土体力学中的符号约定，而不是连续介质力学。常数 a 和 b 将通过测试数据校准得出，且可编写为：

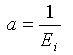     (2)

其中，Ei 是初始切向模量，(σ1 - σ3)ult 是双曲线的渐近值，它通过破坏比率与土体强度相关：

(σ1 - σ3)f = Rf(σ1 - σ3)ult     (3)

很显示，破坏比率 Rf 始终小于 1，且介于 0.75 到 1 之间（由 Duncan 和 Chang 于 1971 年提出）。

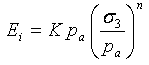     (4)

Duncan-Chang 模型将初始模量定义为：

其中，模量值 K 和模量指数 n 是无量纲材料参数；pa 是公式中用于消除单位制选择效应的大气压力。

土体破坏取决于 Mohr-Coulomb 准则：

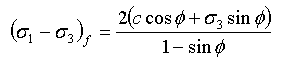     (5)

其中，c 和 φ 是 Mohr-Coulomb 强度参数。对于非凝聚性土体，莫尔包络线通常是弯曲的，变化公式如下：

     (6)

其中，φ0 是围压 σ3 在单位大气压力的摩擦角，Δφ0 是 σ3 增加 10 倍后在 φ 的约简。

切向模量的增量表示公式为：

Et = (1-RfS)2Ei     (7)

其中，S 是应力级别或滑动强度的分数：

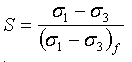     (8)

当 (σ1 - σ3) 小于其历史最大值时，假定土体正在卸载或重新加载，且切向模量定义为：

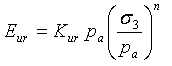     (9)

其中，Kur 是卸载-重新加载模量值，且始终大于主载荷模量值 K。卸载-重新加载的模量指数与主载荷相同。

类似地，在 E-v 模型（由 Kulhawy 和 Duncan 于 1972 年提出）中，初始泊松比可以表示为：

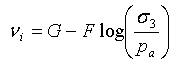     (10)

切线泊松比

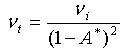     (11)

其中

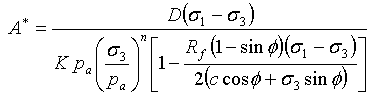     (12)

D、F 和 G 是材料参数。

在 E-B 模型（由 Duncan et al. 于 1980 年提出）中，体积模量表示为：

     (13)

其中，Kb 和 m 分别是体积模量值和体积模量指数。

初始应力：

通常需要考虑土体的初始应力状态。当前，该软件提供了均匀静水压力和自重引起的两类初始应力状态。假定这些初始应力处于静力平衡状态，因此不会影响分析中由外施载荷引起的应力和应变值。换而言之，初始应力不会改变“结果”环境中显示的应力结果，也不会导致任何初始位移。如果这种假设不合适，请明确模拟载荷历史。

稳定性：

尽管在标准的三轴压缩测试中，围压 (σ3) 始终大于 0，但在常规有限元分析中，它可以等于或小于 0。在这种情况下，若要确保分析数值稳定，则需一组初始弹性模量。用户可以在材料属性的“高级”选项卡中指定相应值（静止时的杨氏模量和泊松比）。如果未提供，则默认为 E0 = 0.01K*pa 和 ν0 = 0.499。

土体破坏后（应力级别达到 1），其载荷能力快速流失。若要确保分析稳定，则需一组残余模量。用户可以在“高级”选项卡中指定相应值（破坏时的杨氏模量和泊松比）。如果未提供，则默认为 E1 = 0.001K*pa 和 ν1 = 0.499。这组值还将用作破坏前的弹性模量下限。

有时，上述稳定模量可能会明显影响仿真结果。尽管静止时的弹性模量可通过试验得出，但通常很难确定 Duncan-Chang 模型的正确破坏模量。不过应当指出的是，Duncan-Chang 模型旨在用于破坏前，且在破坏有限且局部出现的情况下可以接受。

限制：

Duncan-Chang 模型成功分析了许多实际问题，且可以通过标准的三轴压缩测试轻松设置。当三轴测试结果不可用时，文献中还提供了大量可用的模型参数。但是，用户应注意到其重要限制（由 Duncan et al. 于 1980 年提出）：

  1. 不考虑中间主应力 σ2；
  2. 发生大范围破坏时，结果可能不可靠。
  3. 不考虑因剪切应力变化引起的体积变化（剪胀）；
  4. 输入参数不是基本的土体属性，而是适用于有效条件范围的经验值。
  5. 该模型主要用于准静态分析。

参考：

  1. Duncan, J. M. 和 Chang, C. Y., Nonlinear analysis of stress and strain in soils, Journal of the Soil Mechanics and Foundations Division, ASCE, 96(SM5), 1629-1653, 1970.
  2. Kulhawy, F. H. 和 Duncan, J. M., Stresses and movements in Oroville Dam, Journal of the Soil Mechanics and Foundations Division, ASCE, 98(SM7), 653-655, 1972.
  3. 3. Duncan, J. M., Byrne, P., Wong, K. S. 和 Mabry, P., Strength, stress-strain and bulk modulus parameters for finite element analysis of stresses and movements in soil masses, Report No.UCB/GT/80-01, Dept.Civil Engineering, U.C. Berkeley, 1980.
父主题： Duncan-Chang 材料属性