針對射出成型零件，零件在模具中會受到約束。射出成型零件凝固期間，可防止凝固層收縮。一旦零件從模具中頂出，這些殘留應力將以收縮變形的形式釋放出來
當凝固層仍在模具中時，有幾種機制可防止凝固層收縮。對模具壁的黏著力可阻止實體層 (至少是外部表層) 移動。新形成的實體表面會透過熔膠壓力的拉伸作用力保持固定。而幾何約束亦扮演非常重要的角色。模擬時會假設零件完全約束在模具中。不考慮零件模具分離和模具內收縮。
凝固期間，母模仁內的殘留應力會增加。鑑於約束抑制的性質，殘留應力分佈主要由改變壓力歷程及凝固層生成決定。一旦零件從模具中頂出，這些殘留應力會以收縮變形的形式釋放出來。如果等於母模仁內殘留應力的初始應變均勻，則零件會均勻收縮，沒有任何翹曲與成型後期殘留應力。翹曲是由整個零件的收縮變化所致。
會考量兩種類型的收縮變化：
- 各區域的收縮變化 (差異收縮效果)
- 針對典型薄壁零件，可將這種形式的收縮變化分為成型零件厚度方向上的變化 (主要由差異冷卻導致) 與各表面區域的變化。
- 不同方向的收縮變化 (配向影響)
- 水平與垂直收縮之間的差異，以及與纖維配向分佈相關的非等向性材料性質是導致纖維充填熱塑零件翹曲的其中一個主要原因。
製程期間，射出成型零件的收縮取決於材料的熱力學行為。為了簡單起見，我們會假設凝固零件中的線性彈性行為與熔膠中的純黏性行為，亦即熱黏彈性材料模型。
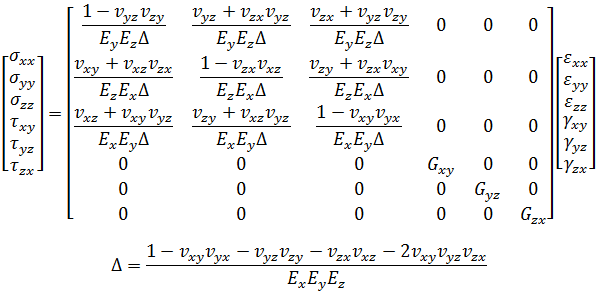
4 節點 1 級四面體元素適用於 3D 流模擬。但是，如果將一級四面體元素用於典型薄壁零件或複雜三維零件薄壁區域的翹曲分析，眾所周知的剪切鎖定問題將使得結構反應非常有勁度 [1]。剪切鎖定或寄生剪切由線性四面體元素的線性位移場不準確所致。縱橫比較大的元素可能使該問題更加嚴重。另一方面，如果要保持較低的計算成本，可能無法避免的會產生高縱橫比的四面體元素。因此，一級四面體元素不適用於射出成型零件的薄壁區域。
已針對 3D 翹曲分析設計混合元素方案。在 3D 實體區域中使用 4 節點 1 級四面體元素，而在薄壁區域中使用 10 節點 2 級四面體元素。在連接薄壁區域與較厚區域的轉換區域中使用轉換 5-9 節點四面體元素。
釋放模具邊界約束之後，就會計算翹曲與模具內殘留應力結果。因為所有變數都是與解決方案中時間為零的初始規劃有關，所以可以自然實作增量的初始應變或應力。以下平衡方程式將在時間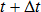 
，針對迭代 k=1、2、3、.... 反覆進行求解。
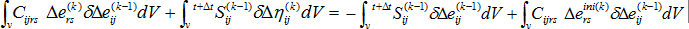
其中：
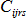是應力-應變張量
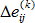和 
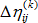是迭代 k 的線性和非線性增量應變張量
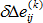和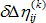 
是對應至虛擬增量位移的線性和非線性增量應變張量
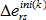是迭代 k 的增量初始應變張量
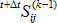是迭代 (k-1) 在時間 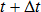之後的第二個 Piola-Kirschoff 應力張量。
如果元素數量較大且薄壁區域也很大，則 3D 翹曲模擬通常尤其需要大量的計算時間。會執行有效的預處理共軛梯度迭代求解器，以減少記憶體需求與計算時間。
參考文獻：
[1] K.J. Bathe, Finite Element Procedures, Prentice Hall Inc.(1996).
[2] S.G.Advani and C.L.Tucker III, The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites, J. Rheol., 31,751-784(1987).
[3] G.P.Tandon and G.J.Weng, The Effect of Aspect Ratio of Inclusions on the Elastic Properties of Unidirectional Aligned Composites, Polym. Compos. 5(4),327-333(1984).
[4] R.A.Schapery, Thermal Expansion Coefficients of Composite Materials Based on Energy Principles.J. Compos. Mater., 2, No.3, 380-404, (1968).