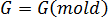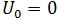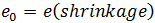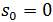應力分析以從翹曲分析中確定的撓曲零件為基礎。
我們將此稱為"「初始條件分析」。"此分析使用從翹曲分析中確定的撓曲與收縮應變做為應力分析的起點。
初始條件分析適用於之前內容中所描述的三種分析類型中的每一種分析類型。在此部分內容中,我們將先描述如何將翹曲結果傳遞到應力分析,然後對應如何搭配主要分析類型使用初始條件分析進行討論。這包括:小型撓曲、挫曲、大型撓曲與模態頻率分析。
如果我們這樣寫:
-
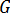 = 模型幾何圖形
= 模型幾何圖形 -
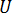 = 位移
= 位移 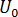 = 初始位移
= 初始位移 -
 = 應變
= 應變 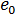 = 初始應變
= 初始應變 -
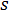 = 應力
= 應力 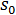 = 初始應力
= 初始應力
我們便可依照以下方式對翹曲的輸入與初始條件應力分析進行比較:
翹曲分析:
初始條件應力分析:
上述內容中需要注意的關鍵點是,並不會使用初始應力來實現「翹曲中的殘留應力」,""而是會憑藉 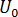 與
與 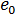 來實現。在應力分析的第一個步長中,FENAS 會有效重複在翹曲分析的最後一個步長完成的應力計算。這裡面並沒有負擔,因為應力始終在大型撓曲分析開始時計算。
來實現。在應力分析的第一個步長中,FENAS 會有效重複在翹曲分析的最後一個步長完成的應力計算。這裡面並沒有負擔,因為應力始終在大型撓曲分析開始時計算。
另一種 (簡單的) 方法是將翹曲的形狀
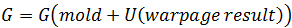
與初始應力 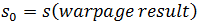 傳遞至初始條件應力分析。
傳遞至初始條件應力分析。
如上所述的使用方法可達成相同的效果,但具有下列優點:
-
在兩種分析中都會使用一致的應變定義 (應變=變形/長度),因為幾何圖形資料 (
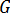 ) 不會改變。為了闡明這一點,已使翹曲的零件負載為零。採用的方法預測為零回應 - 即沒有移動。由於應變定義的改變,這並不屬於初始應力方法的情況,也就是說,應力有"「人為重新分佈」可以處理定義的改變。"
) 不會改變。為了闡明這一點,已使翹曲的零件負載為零。採用的方法預測為零回應 - 即沒有移動。由於應變定義的改變,這並不屬於初始應力方法的情況,也就是說,應力有"「人為重新分佈」可以處理定義的改變。" -
您可以減少應力分析中的彈性模數,以輕鬆降低翹曲分析中的殘留應力。減少的彈性模數可在應力分析中使用,以概略模擬翹曲中殘留應力的鬆弛影響,並考慮到負載下的潛變 (可使用「有效的線性模數)。""
例如,如果您針對翹曲使用 E1=1600 與 E2=1200 MPa,並針對外部負載使用 E1=800 與 E2=600 MPa,則在外部負載分析的第一個步長開始時計算的應力為在翹曲分析結束時的殘留應力輸出的一半。因此您可以將"「降低的殘留應力」傳遞到外部負載分析中。"在初始應力方法中,這不會那麼容易。
-
後處理將會簡化,因為無須將初始應力加入結構或翹曲分析中的應力,來產生最終應力。
初始條件與三種分析類型
此部分內容包含一些有關搭配每一種分析類型使用初始條件分析的特定註解。
- 挫曲分析
-
當執行挫曲分析時,會執行兩種分析;先執行小型撓曲分析,然後執行挫曲分析。
一般會使用線性 (傳統) 挫曲方法。會使用初始小型撓曲分析來確定 100% 負載時的零件構形。然後挫曲分析會使用 0 與 100% 負載時的已知構形。當對結果進行後處理時,您可以檢查 100% 負載時的撓曲形狀,以及從挫曲分析中確定的模式形狀。
但是,針對具有初始條件的挫曲分析,無法將傳統線性挫曲理論套用至問題上,因為應力在套用負載之前非為零。因此必須使用"「線性化挫曲」方法。"在此方法中,會使用初始小型撓曲分析來確定負載百分比非常小的時候的零件構形。然後線性化挫曲分析會使用 0% 及小步長結束時的已知構形。
註: 這表示當對初始條件挫曲分析結果進行後處理時,無法使用 100% 負載時的撓曲形狀。您只能顯示模式形狀。如果您需要線性結果,您將必須執行小型撓曲分析與挫曲分析。
由於從挫曲分析中確定的模式形狀是增量模式形狀 (挫曲點的構形改變),因此必須將它加到翹曲形狀上 (在適當的比例調整之後)。
- 大型撓曲分析
-
註: 大型撓曲初始條件應力分析只能對大型撓曲翹曲結果執行。
大型撓曲翹曲分析結果只能在已知翹曲結果為高線性時,也就是當挫曲分析中的特徵值非常高時使用。
- 模態頻率分析
-
模態頻率分析也可使用翹曲分析中的初始條件。與挫曲分析的註解類似的註解也適用於此情況。
包括初始條件的影響
翹曲中的應力可能會對負載下零件的回應產生穩定或不穩定的影響。例如,如果殘留應力導致細長表面的壓縮,則也會將其有效加入到壓縮負載所導致的應力。在此情況下,不包含初始條件的分析會過度預測失敗負載。
另外,如果翹曲應力導致產生張力,壓縮負載可能會抵銷殘留應力,使不包含初始條件的分析對失敗負載做出太過保守的預測。
指定的位移與初始條件
軟體有一項有用的功能,就是指定初始條件中的位移 (而非套用負載)。這可以讓您確定使翹曲形狀變形為已知構形的所需力度。最終結果也將展示迫使零件成為該構形所導致產生的應力。
針對已套用指定位移邊界條件的每一個節點,FENAS 將在結果摘要檔案中輸出「"反應力"」。
可以將應力結果做為初始條件使用嗎?
以下兩個範例說明何時根據應力分析準備初始條件分析是有用的:
-
已使用指定位移應力分析迫使翹曲零件成形。之後您可尋找該零件對進一步外部負載的回應。
-
已將外部負載套用於零件。之後您可尋找該零件對熱負載的回應。
但是,由於以下原因,您無法在此版本中使用結構結果做為其他應力分析的初始條件。
翹曲分析結果可做為應力分析的初始條件使用,因為應力分析中的約束反應接近零。針對外部負載的應力分析,其中的約束反應全都為非零,必須將這些反應傳遞至第二分析。若未傳遞這些反應,可能會違反平衡需求,特別是當約束移動時。
在此版本中,沒有機制可將約束反應從第一分析傳遞至第二分析。因此,應力分析程式將不允許您使用應力分析結果檔案做為初始條件。