不穩定翹曲會導致元件發生挫曲。不可再將總撓曲三個收縮變量中每一個的比重假定為線性。
在此情況下,會使用所謂的敏感度分析。此功能僅適用於「中間平面」分析技術。
敏感度分析的目標是針對收縮中的已知變更確定負載係數的變更。負載係數會指示實際套用負載 (若為收縮分析,則為零件內部負載) 的係數,零件翹曲會變得不穩定,進而導致挫曲。負載係數小於 1 表示實際負載足以導致零件發生挫曲。負載係數大於 1 表示當決定以高於實際負載的負載大小開始挫曲時翹曲穩定。
假定可以單獨改變收縮元件,則可以將負載係數 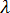 視為這些元件的函數,即
視為這些元件的函數,即 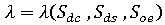
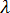 視為這些元件的函數,即
視為這些元件的函數,即 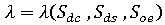
若要解決翹曲問題,我們希望知道要變更以增加負載係數 (即使翹曲穩定) 的元件。執行此作業的一種方式為取得與每個元件相關之 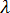 的部份導數。遺憾的是,無法以分解的方式執行此作業,因為沒有將
的部份導數。遺憾的是,無法以分解的方式執行此作業,因為沒有將 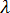 與元件相關聯的已知函數。但會大致估計部分導數。
與元件相關聯的已知函數。但會大致估計部分導數。
假設使用總體收縮的挫曲分析的負載係數為 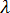 。現在,將其中一個收縮元件增加一定的量 (比如
。現在,將其中一個收縮元件增加一定的量 (比如 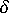 ),以得到一個新的總體收縮 S'。例如,如果我們增加差異收縮元件,便會得到:
),以得到一個新的總體收縮 S'。例如,如果我們增加差異收縮元件,便會得到: 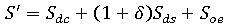
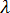 。現在,將其中一個收縮元件增加一定的量 (比如
。現在,將其中一個收縮元件增加一定的量 (比如 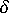 ),以得到一個新的總體收縮 S'。例如,如果我們增加差異收縮元件,便會得到:
),以得到一個新的總體收縮 S'。例如,如果我們增加差異收縮元件,便會得到: 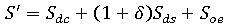
如果在挫曲分析中使用此 S' S' 值來取得新負載係數 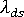 ,則與差異收縮元件相關之
,則與差異收縮元件相關之 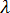 的導數約為:
的導數約為: 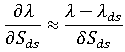
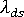 ,則與差異收縮元件相關之
,則與差異收縮元件相關之 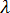 的導數約為:
的導數約為: 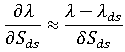
如以下影像所示:
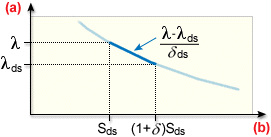
以收縮函數表示的負載係數
.(a) 負載係數,(b) 收縮
值 (1 + 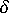 ) 稱為靈敏度係數,該係數為一項程式輸入。
) 稱為靈敏度係數,該係數為一項程式輸入。
上述內容適僅用於一個元素。針對真實零件,每個元素都有一個 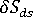 值。為了處理此情況,會將各種元素變更合併為單一的收縮變更測量。這些變更的範數會用於元素收縮以取得單一值,該值會在分析記錄中報告為「收縮變更範數」。
值。為了處理此情況,會將各種元素變更合併為單一的收縮變更測量。這些變更的範數會用於元素收縮以取得單一值,該值會在分析記錄中報告為「收縮變更範數」。
此範數定義為如下方程式: 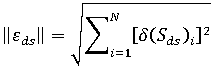
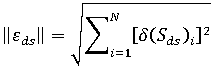
其中 N 是模型中的元素數。
同樣地,會分別計算差異冷卻與配向性影響變量的負載係數敏感度。
則「收縮變更範數」是每個元素收縮變更平方的總和,會用於翹曲挫曲的敏感度分析。