當將熱塑、半結晶材料與適當結晶形態性質資料一起使用時執行結晶分析的選項已實施。
結晶動力學塑型
結晶動力學塑型，包括流動增強結晶，以及在剪切流期間及之後因流動而引起的半結晶材料形態變更，已在熱塑流求解器中實施。
未見結晶生成率受材料流動的顯著影響。因此，我們假設生成率僅取決於溫度，並遵循 Hoffman-Lauritzen 理論[1]：
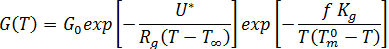
其中
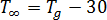，以及 
。
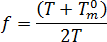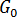和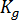 
為材料等級特定常數，其可於靜態條件下確定，
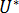為運動的啟用能量，
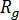為氣體常數，
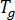為玻璃轉換溫度，
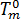為材料等級特定平衡熔膠溫度，其假設為僅取決於壓力。會選擇線性函數來描述壓力相依性[2]：
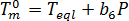
其中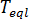 
為平衡熔膠溫度，
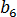為材料之 PVT 模型的等級特定常數，P 為壓力。
核產生表示為：
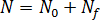
其中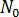 
是靜態條件下已啟用的核數，
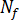是流動所引發的已啟用核數。
在靜態條件下啟用的核數假設為超冷卻溫度的唯一函數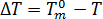 
，且由以下方程式描述[3]：
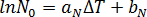
其中 
和 
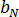為材料等級特定常數。
有關結晶流動的影響，其考慮因素為使過量自由能量和流動引起的配向與結晶動力學相關聯。流動引起的核數由下列微分方程得出：
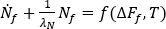
其中
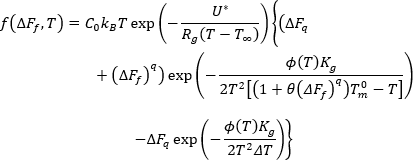
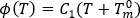，以及
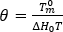
結晶性的開發會導致黏度增加，並最終導致凝固。已在模擬中採用增強係數來描述在以下黏度下的結晶性影響[4]：
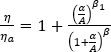(若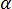 
< 
)。
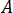此處的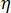 
是整個系統的黏度，
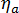是非結晶階段的黏度，
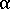是相對結晶性。
參考文獻
[1]S.I. Lauritzen and J. D. Hoffman, ''Theory of formation of polymer crystals with folded chains in dilute solution,'' J. Res. Natl. Bur. Stand. 64A, 73-102 (1960)
[2] R. Fulchiron, E. Koscher, G. Poutot, D. Delaunay, and G. Regnier, ''Analysis of the pressure effect on the crystallization kinetics: dilatometric measurements and thermal gradient modelling,'' J. Macromol. Sci., Phys. 40, 297-314 (2001)
[3] E. Koscher and R. Fulchiron, ''Influence of shear on polypropylene crystallization: morphology development and kinetics,'' Polymer 43, 6931-6942 (2002)
[4] R. Zheng and P. K. Kennedy, "A model for post-flow induced crystallization: General equations and predictions", J. Rheol., 48(4), 823-842 (2004)