模態頻率分析

模態頻率分析用於定義結構的自然、無衰減的頻率響應。

理論上，這與挫曲分析類似，但對於結果的實際詮釋不同。

結構的動態回應可由以下方程式表示：

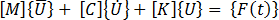
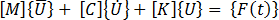
其中：

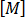• 是質量矩陣，
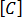• 是衰減矩陣，
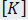• 是勁度矩陣，
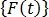• 是可能取決於時間的強制函數的向量，
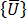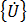• 、 和 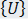、 與 分別是節點加速度、速度與位移的向量。

如果我們考慮透過將衰減矩陣與強制函數的向量設定為零所取得的無衰減及無強制結構的方程式，而不是此一般方程式，則以下方程式：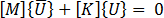

此方程式定義結構的基本回應，並可用於求出共振頻率。為了證明這一點，請注意以上方程式的解可以寫成以下形式：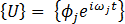

其中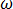， 是震動頻率。

使用以上方程式取代它前面的方程式，將得出：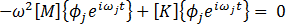

亦即，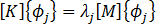

其中，。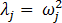

這是標準特徵值問題。其可使用子空間迭代方法來求解。

具有 n 自由度的結構將會有 n 個特徵向量。針對每個特徵值 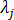， 都有對應的一個特徵向量 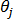， 通常稱為模式形狀。實際上，並不需要確定所有特徵值。一般而言，求出最低的幾個特徵值就足夠了，因為這些特徵值可以支配結構的回應。應力分析程式可讓您輸入要求出的特徵值數。此外，當計算特徵值數時，可執行 Sturm 序列檢查來檢查特徵值是否連續。