殘留應變收縮預測方法是 Autodesk Moldflow 在其「翹曲」分析產品中使用的兩種收縮預測方法中較舊的一種。
殘留應變方法以下列收縮的經驗模型為基礎:
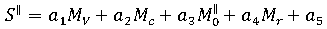
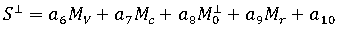
其中,
-
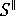 和
和 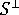 分別為平行及垂直於流動方向的線性收縮的預測值,
分別為平行及垂直於流動方向的線性收縮的預測值,
- a1, ...,a10 為指定材料的常數,
- Mv 是對體積收縮的測量,
- Mc 是對結晶的測量,
-
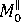 ,
, 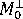 是對平行及垂直於流動方向的分子配向的測量,
是對平行及垂直於流動方向的分子配向的測量,
- Mr 是對模具限制的測量。
係數 a1, ...,a10 為指定材料的常數,由收縮特性程序確定,於此,會將透過對標準測試零件執行成型而取得的實驗性收縮資料套用至上述方程式。
針對指定的翹曲模擬,可以使用「充填與保壓」分析計算模型中的各種測量 (體積收縮、結晶、材料配向與模具限制)。以下部分會對這些測量進行更詳細的描述。
根據「冷卻」分析的決定,由於模具一側與另一側的溫度有差異,因此已延伸上述收縮模型來說明彎矩。合併這些影響會導致每個元素的頂部與底部,在平行及垂直於流動方向上收縮。下面的「模具限制項」部分會對模型的此方面進行描述。
體積收縮項
體積收縮是收縮計算的基本部分。影響體積收縮的主要因素為熔膠的保持壓力與溫度歷程。您可以使用保壓與冷卻期間經歷的溫度/壓力歷程,來根據材料的「平衡」pvT 關係,計算每個元素的體積收縮。""
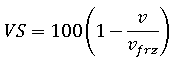
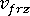 為元素中的聚合物完全凝固,或元素中的熔膠壓力變為大氣壓力時,聚合物的比容; 為大氣壓力與室溫下,聚合物的比容。會使用 pvT 關係來計算特定壓力與溫度下的特定體積。
為元素中的聚合物完全凝固,或元素中的熔膠壓力變為大氣壓力時,聚合物的比容; 為大氣壓力與室溫下,聚合物的比容。會使用 pvT 關係來計算特定壓力與溫度下的特定體積。
結晶項
平衡 pvT 資料不足以描述半結晶材料的體積收縮。這些材料中發生的體積收縮量也取決於結晶度。零件中的結晶度主要受模具溫度的影響。由於結晶性等級,收縮計算會使用材料的結晶動力學來決定體積收縮。
結晶是溫度和時間共同的函數。結晶等級由冷卻率決定。快速冷卻率與較低級別的結晶性大小相關聯,反之亦然。
在射出成型零件中,較厚區域通常比較薄區域冷卻得慢,因此結晶度和體積收縮較大。從另一方面來講,較薄區域的冷卻速度非常快,因此其結晶度與體積收縮都比根據平衡 pvT 資料預測的低。
配向項
剪切流期間,聚合物分子將沿流動方向自行對齊。此配向範圍取決於材料承受的剪切率和熔膠溫度。
材料停止流動時,誘導分子配向開始以一定速率鬆弛,該速率取決於材料鬆弛時間。如果材料在完成鬆弛前凝固,則分子配向為「凝固」。""此凝固配向將會導致平行及垂直於材料配向方向的方向上發生不同等級的收縮。
若要決定凝固配向的等級,「充填與保壓」分析會計算每個元素以下項目的數量,並在網格點凝固時計算該元素上的每個網格點 i:
- 剪應力
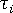
- 冷卻率
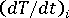
- 流動角度
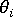 ,相對於元素的局部 X 軸。局部 X 軸是元素的定義中,從第一個節點編號到第二個編號的方向。請注意,層壓板之間的流動方向可能有所不同,因為凝固層的生成可能會變更流動通道,並因此變更流動方向。
,相對於元素的局部 X 軸。局部 X 軸是元素的定義中,從第一個節點編號到第二個編號的方向。請注意,層壓板之間的流動方向可能有所不同,因為凝固層的生成可能會變更流動通道,並因此變更流動方向。
決定「凝固」配向最終等級的方法是,採用材料停止流動時的分子配向等級 (與此時的剪應力成比例),並在一定程度 (由材料的鬆弛特性決定) 上降低配向等級 (為冷卻率的函數)。""
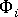 之後,可以使用以下方程式計算
之後,可以使用以下方程式計算 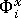 網格點 i 處,與局部 X 軸平行的方向上的配向測量 :
網格點 i 處,與局部 X 軸平行的方向上的配向測量 :
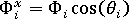
垂直方向上的配向測量 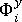 將透過類似方式確定。
將透過類似方式確定。
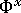 與
與 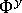 ) 做為一個整體進行確定,即
) 做為一個整體進行確定,即
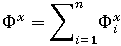
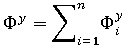
其中,n 是塑膠中的網格點數。
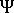 定義為:
定義為:

模具限制項
當零件位於模具中時,假設它無法在元素的平面中實際收縮。但是,允許厚度方向上的收縮。
材料收縮時,會在零件中產生殘留應變。充填、保壓與冷卻階段的塑膠元素溫度歷程會影響解除這些應力的速率。您可以從一些較小的溫度增量 (其中,鬆弛速率由目前溫度決定) 加入比重,來計算模具限制的測量。
等效熱應變
上述殘留應變收縮模型會為每個元素提供平行及垂直收縮的值,以表示該元素整個厚度的平均值。實際上,收縮等級在厚度範圍內會有所不同。如果母模仁中心線周圍的此收縮分佈非對稱,則會產生彎矩,進而可能影響零件的翹曲。
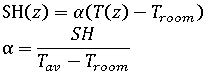
其中:
T(z) 是中心凝固時 (即元素完全凝固時),根據「冷卻」分析獲得的塑膠中的溫度分佈。T(z) 的峰值是材料的凝固溫度,且位於根據「冷卻」分析決定的元素整個厚度上的某個位置。計算上述方程式時,每個模具母模仁介面的溫度與週期結束時的模具溫度近似,且會以拋物線曲線大致表示最大溫度任意側的溫度分佈。
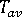 是厚度上的平均 T(z),
是厚度上的平均 T(z),
SH 是根據收縮模型預測的平均收縮,
SH(z) 是熱膨脹的「有效」係數。""它並不是純熱膨脹係數,因為它包括其他收縮程序 (如結晶性) 的影響。
然後會線性化此 SH(z) 分佈,即以保留分佈的折彎影響的方法,將其轉換為直線。折彎影響具有以下積分特性:
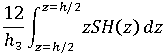
其中,h 是元素厚度。
請注意,向直線轉換不是一種逼近,而是一種必然,因為 Autodesk Moldflow 應力分析程式 (像是大多數應力分析程式) 支援的元素類型只能處理整個元素厚度上的線性應力分佈。
此線性化的結果是直線收縮分佈 SHL(z)。會使用上述方程式,將其轉換回線性化溫度分佈 TL(z)。轉換回溫度分佈的原因具有歷史性;ABAQUS 只接受熱膨脹與溫度變化係數,不是直接的初始應變輸入。
由 TL(z) 確定的元素頂部與底部溫度、室溫,以及平行與垂直方向上的 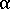 值都會另存成「翹曲」分析的輸入。在「翹曲」分析中,會在此部分開始處使用這兩個方程式,來根據這些值重新建構 SHL(z)。
值都會另存成「翹曲」分析的輸入。在「翹曲」分析中,會在此部分開始處使用這兩個方程式,來根據這些值重新建構 SHL(z)。