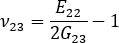纖維配向是確定機械 (彈性) 強度及成型零件勁度的主要因素之一。
目前已發展出一些理論,來在已知零件中的纖維配向分佈時,預測短纖維複合物的機械性質。
若要計算機械性質,所有理論都依照一個兩步驟的程序操作:
- 預估單向短纖維強化材料的性質。
- 然後根據纖維配向分佈計算出這些性質的平均值。
因此,這種方法可單獨說明纖維長度與纖維配向的影響。
Tandon-Weng 模型是計算複合材料等向性母體之單向性機械性質的基礎。Autodesk Moldflow Insight 實作也會考慮 Tucker/Liang 對 Tandon-Weng 模型進行蒲松氏比計算的處理方式。
需要輸入到分析中的纖維與聚合物性質有:
-
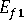 (纖維的縱向模數)
(纖維的縱向模數)
-
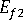 (纖維的橫向模數)
(纖維的橫向模數)
-
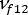 (纖維的縱向蒲松氏比)
(纖維的縱向蒲松氏比)
-
 (纖維的縱向剪切模數)
(纖維的縱向剪切模數)
-
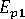 (聚合物的縱向模數)
(聚合物的縱向模數)
-
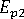 (聚合物的橫向模數)
(聚合物的橫向模數)
-
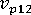 (聚合物的縱向蒲松氏比)
(聚合物的縱向蒲松氏比)
-
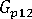 (聚合物的縱向剪切模數)
(聚合物的縱向剪切模數)
-
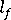 (平均纖維長度)
(平均纖維長度)
-
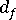 (平均纖維直徑)
(平均纖維直徑)
-
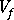 (纖維的體積分率)
(纖維的體積分率)
下列基本機械性質針對複合材料中的每一個元素導出:
-
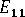 (縱向模數)
(縱向模數)
-
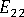 (橫向模數)
(橫向模數)
-
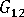 (平面內剪切模數)
(平面內剪切模數)
-
 (平面外剪切模數)
(平面外剪切模數)
-
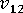 (平面內蒲松氏比)
(平面內蒲松氏比)
-
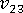 (平面外蒲松氏比)
(平面外蒲松氏比)
縱向與橫向模數
Tandon-Weng 模型會將短纖維強化複合物視為嵌入於無限彈性聚合物母體中的單向對齊球體包含物的特殊情況處理。
單軸對齊系統的縱向模數可以寫為:
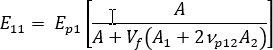
其中,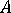 、
、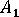 和
和 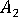 為與 Tandon Weng 論文中參數相關的參數。
為與 Tandon Weng 論文中參數相關的參數。
單軸對齊系統的橫向模數可以寫為:
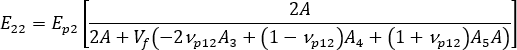
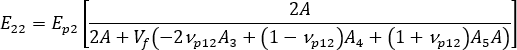
其中 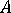 、
、 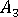 、
、 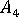 與
與 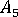 為與 Tandon 和 Weng 論文中的參數相關的參數。
為與 Tandon 和 Weng 論文中的參數相關的參數。
剪切模數及蒲松氏比
單軸對齊系統的縱向剪切模數可以寫為:
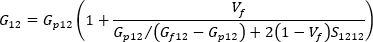
而單軸對齊系統的橫向剪切模數可以寫為:
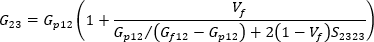
其中 S1212 和 S2323 為 Eshelby 之張量的對應分量,在 Tandon 和 Weng 的論文中提供其解析解。
單軸對齊系統的平面內蒲松氏比可以寫為:
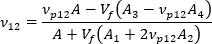
單軸對齊系統的平面外蒲松氏比可以從複合模數明確計算為: