Appendix A: NURBS Geometry

There are quite a few really good books on spline geometry and NURBS geometry. This appendix will not try to teach you everything about NURBS but will try to give you a general overview of the Maya particulars.

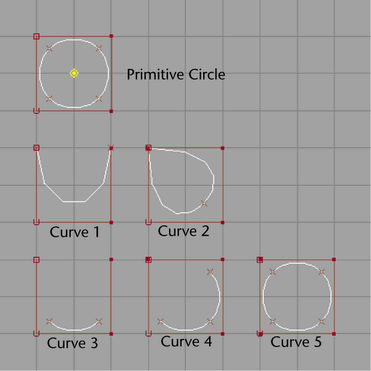
Of the six curves in the illustration, the first is a circle primitive with four spans. Notice how the circle does not touch the hull. The next five curves are attempts at replicating this geometry using the curve building tools in Maya.

The circle appears to have four CVs using the default options of the curve tool (Create > CV Curve Tool), with the following options set:

If you place four CVs, you produce something that looks like "Curve 1". This is an Open curve. It’s open because the curve has a gap between the first and last CVs. It also has only one span, where the circle has four. (A span connects two edit points.)

If you try to close the curve by placing another CV on top of the first CV, you produce something that looks like Curve 2. Curve 2 is closer to the primitive circle, first because it is Closed, that is, there is no gap in the curve between the first and last CVs, and second, because it has two spans. However, you will notice that the curve does not look like a circle, it intersects the hull at the first CV and there is a discontinuity in the curve’s tangent at this point. If you were to place another CV overlapping the second CV, you would find that the curve is now open and looks even less like a circle. A third and fourth CV don’t help either, all because the first and last CVs are always on the hull.

If you go into the curve tool’s option box and turn off Multiple End Knots and place four CVs, you produce a curve which looks like Curve 3. This looks more promising than Curve 1 since the curve does not intersect the hull. If you now place a fifth CV on top of the first CV you produce Curve 4. This still looks promising. If you go further and add a sixth and seventh CV on top of the second and third CV, you produce Curve 5. This looks exactly like the circle. You’ve done it.

Well, not quite. If you were now to pull one of these additional CVs away from the CV under it, you would pull the curve apart, producing an open curve again. However, no matter how you pull the CVs on the circle you cannot pull it apart, it remains a closed curve. So there is still a small difference between these two curves. The difference is the form of the curve. Curves 1, 3 and 4 are all Open, that is, their form is open. Curves 2 and 5 are closed, that is, their form is closed. The circle is neither open nor closed, it’s form is a third type, called periodic. Periodic implies that the last degree CVs of the curve overlap the first degree CVs, and all operations on the CVs ensure that they stay together and cannot be pulled apart.

A periodic curve generally has tangency continuity on the whole curve while a closed curve will not.

#include <maya/MSimple.h>
#include <maya/MIOStream.h>
#include <maya/MPointArray.h>
#include <maya/MDoubleArray.h>
#include <maya/MFnNurbsCurve.h>
MStatus curveTest( const MArgList& )
{
     MFnNurbsCurve curveFn;
     const double cvs[][4] = {
                                 { -1, 0, -1, 1 },
                                 { -1, 0,  1, 1 },
                                 {  1, 0,  1, 1 },
                                 {  1, 0, -1, 1 }
                             };
     const double knots[] = { 0, 0, 0, 1, 1, 1 };
     MPointArray cvArray( cvs, unsigned( sizeof(cvs) / (4*sizeof(double)) ) );
     MDoubleArray knotArray( knots, unsigned(sizeof( knots )/sizeof( double )) );
     MStatus status;
     MObject curve = curveFn.create( cvArray, knotArray, 3, MFnNurbsCurve::kOpen,
     false, false, MObject::kNullObj, &status );
     if ( MS::kSuccess != status )
     {
         cout << "Failed to create curve\n";
         return status;
     }
     return MS::kSuccess;
}
     DeclareSingle( curveTest );

const double knots[] = { 0, 1, 2, 3, 4, 5 };

const double cvs[][4] = {
                            { -1, 0, -1, 1 },
                            { -1, 0,  1, 1 },
                            { 1,  0,  1, 1 },
                            { 1,  0, -1, 1 },
                            { -1, 0, -1, 1 }
                        };
const double knots[] = { 0, 0, 0, 1, 2, 2, 2 };

const double cvs[][4] = {
                            { -1, 0, -1, 1 },
                            { -1, 0,  1, 1 },
                            {  1, 0,  1, 1 },
                            {  1, 0, -1, 1 },
                            { -1, 0, -1, 1 }
                        };
const double knots[] = { 0, 1, 2, 3, 4, 5, 6 };

const double cvs[][4] = {
                             { -1, 0, -1, 1 },
                             { -1, 0,  1, 1 },
                             {  1, 0,  1, 1 },
                             {  1, 0, -1, 1 },
                             { -1, 0, -1, 1 },
                             { -1, 0,  1, 1 },
                             {  1, 0,  1, 1 }
};
const double knots[] = { 0, 1, 2, 3, 4, 5, 6, 7, 8 };

MObject curve = curveFn.create( cvArray, knotArray, 3,
 MFnNurbsCurve::kPeriodic, false, false, MObject::kNullObj, &status );

 Except where otherwise noted, this work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. Please see the Autodesk Creative Commons FAQ for more information.