このセクションでは、一方向および織物複合材料の複合材料両方の平均応力とひずみ状態の概念について説明します。
これらの数量の簡単な計算を展開し、構成の平均数量を使用した場合の利点と制限について説明しています。
σ(x,y,z)は、異種ミクロ構造の各構成材料内のそれぞれの位置に応じて異なる実際の応力テンソル場を示します。D は、1 点の複合材料応答を特徴づけるのに十分な代表体積要素(RVE)の領域を示します。RVE 内の実際の応力分布の複雑さに関係なく、RVE 内の複合材料の平均(または均質化)応力状態 σc は、次のように表すことができます。

ここで、V は RVE の総体積です。同様に繊維と母材の平均応力状態は、次のように表すことができます。

ここで、Vf および Vm は、RVE 内の繊維および母材の体積をそれぞれ示します(V=Vf +Vm)。さらに、Df および Dm は、RVE 内の繊維および母材構成が占めるサブ領域をそれぞれ示します(D = Df 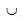 Dm)。方程式 1-3 を結合すると次の方程式になります。
Dm)。方程式 1-3 を結合すると次の方程式になります。

ここで φf = Vf/V および φm = Vm/V は繊維と母材の構成材料の体積分率をそれぞれ示します。
同様の論理をひずみテンソルに適用して、次の方程式 5~8 を生成します。

多重連続体理論で使用する基本的な論点は、構成の平均応力とひずみ状態(σf、σm、εf、εm)は、複合材料の平均応力とひずみ状態(σc、εc)よりも、損傷の進展と材料破損の予測でより関連性が高いということです。母材構成の損傷の進展と破損は、物理的に母材構成材料の応力とひずみにより促進されるもので、繊維構成材料の応力とひずみ、または均質化された複合材料の応力とひずみによって促進されるものではありません。同様の論点は繊維構成に関しても言えます。
複合材料の損傷の進展と破損を予測するために、優れた情報を提供する個別の構成上の実際のマイクロメカニカル応力場を平均化して評価することは簡単ですが、体積の平均化プロセスにはさまざまな平均応力状態が関連するため、その特性のフィルタリングを検討することが有益です。単純な均質化された複合材料の応力状態 σc に影響される、一方向繊維強化複合材料の代表体積要素を考慮することから開始しましょう。たとえば、単軸応力状態、ここで 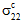 > 0 およびその他すべての
> 0 およびその他すべての 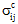 = 0 です。複合材料の平均応力状態が単軸であっても、RVE の異種ミクロ構造内の実際のマイクロメカニカル応力場 σ(x,y,z)は非常に複雑です。これは、剛性、ポアソン比、および熱膨張係数の違いによって発生する構成材料間の自己平衡化相互作用によるものです。たとえば、実際のマイクロメカニカル応力場の 6 つの応力成分のうち 4 つ( σ11、σ22、σ33、σ23)は、RVE 内で非ゼロ値を達成します。さらに、これらの 4 つの応力成分は、多数のローカルの応力集中を伴って RVE 上で高い空間的変化を示します。ただし、実際の応力成分のうち 3 つ(σ11、σ33、σ23)は、完全に構成材料間の自己平衡化相互作用によるものです。たとえば、繊維と母材ののポアソン比に違いは、σ11(x,y,z)および σ33(x,y,z)場の自己平衡化を促進する原因となります。空間的変化 σ11(x,y,z)、σ22(x,y,z)および σ33(x,y,z)場の存在により、ローカルの平衡を維持するためにせん断応力を発生させる必要があります。方程式 9~11 は、すべての応力成分が繊維方向(つまり、'1' 方向)に対して一定である一方向複合材料 RVE の現在の例のために簡素化された平衡の偏微分方程式を示します。
= 0 です。複合材料の平均応力状態が単軸であっても、RVE の異種ミクロ構造内の実際のマイクロメカニカル応力場 σ(x,y,z)は非常に複雑です。これは、剛性、ポアソン比、および熱膨張係数の違いによって発生する構成材料間の自己平衡化相互作用によるものです。たとえば、実際のマイクロメカニカル応力場の 6 つの応力成分のうち 4 つ( σ11、σ22、σ33、σ23)は、RVE 内で非ゼロ値を達成します。さらに、これらの 4 つの応力成分は、多数のローカルの応力集中を伴って RVE 上で高い空間的変化を示します。ただし、実際の応力成分のうち 3 つ(σ11、σ33、σ23)は、完全に構成材料間の自己平衡化相互作用によるものです。たとえば、繊維と母材ののポアソン比に違いは、σ11(x,y,z)および σ33(x,y,z)場の自己平衡化を促進する原因となります。空間的変化 σ11(x,y,z)、σ22(x,y,z)および σ33(x,y,z)場の存在により、ローカルの平衡を維持するためにせん断応力を発生させる必要があります。方程式 9~11 は、すべての応力成分が繊維方向(つまり、'1' 方向)に対して一定である一方向複合材料 RVE の現在の例のために簡素化された平衡の偏微分方程式を示します。

方程式 10 と 11 は、せん断応力成分 σ23 が、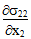 または
または 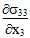 が非ゼロである RVE 内の任意の点で展開する必要があることを意味します。残念ながら、これらの自己平衡化応力成分(σ11、σ33、σ23)は、RVE 上のマイクロメカニカル応力場の平均化プロセスによって完全に除外されます。これにより複合材料の平均応力状態は
が非ゼロである RVE 内の任意の点で展開する必要があることを意味します。残念ながら、これらの自己平衡化応力成分(σ11、σ33、σ23)は、RVE 上のマイクロメカニカル応力場の平均化プロセスによって完全に除外されます。これにより複合材料の平均応力状態は 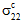 > 0 で単軸となります。
> 0 で単軸となります。
複合材料の平均応力状態 σc が自己平衡化応力成分を表現できないことは、均一な温度変化を受ける拘束のない複合材料の場合に最も良く示されます。この例では、実際の応力場 σ (x,y,z)の 4 つの非ゼロ成分がすべて(σ11、σ22、σ33、σ23)、2 つの構成材料の熱膨張係数の違いが原因で自己平衡化しています。複合材料の平均応力状態は、一様にゼロです(σc= 0)。ただし、大きな温度変化に対しては、実際のマイクロメカニカル応力場 σ(x,y,z)の非ゼロ成分(σ11、σ22、σ33、σ23)が実際に損傷の進展または材料破損を引き起すのに十分に大きい場合があります。
複合材料の平均応力状態の計算中に行われる厳密なフィルタリングとは対照的に、構成の平均応力状態の計算プロセスは、その特定の構成材料に対して自己平衡化する応力成分のみを除外します。構成のポアソン比または熱膨張係数の違いによって促進される自己平衡化垂直応力は、RVE 全体に対して自己平衡化しますが、どの 1 つの構成に対しても自己平衡化しないことに留意してください。したがって、構成の平均応力状態は、これらの自己平衡化垂直応力を除外しません。一方、ローカルの平衡を維持するために発生した自己平衡化せん断応力は、個別の構成材料内でも自己平衡化を行います。したがって、複合材料の平均応力状態と構成の平均応力状態はどちらも自己平衡化せん断応力を除外します。
次のリストは、上記の説明に基づいて構成の平均応力状態のフィルタリング特性をまとめたものです。
- 一般的に、1 つまたは複数の複合材料の垂直応力(例、
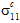 、
、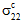 、または
、または 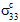 )を適用すると、三軸(つまり、3 つの垂直応力がすべて非ゼロ)の構成の平均応力状態が生成されます。この観察は、複合材料の応力状態が単軸の場合にも当てはまります(例、
)を適用すると、三軸(つまり、3 つの垂直応力がすべて非ゼロ)の構成の平均応力状態が生成されます。この観察は、複合材料の応力状態が単軸の場合にも当てはまります(例、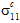 ≠ 0、およびその他のすべての
≠ 0、およびその他のすべての 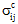 = 0)。これは、構成材料間のポアソン比の相互作用の直接的な結果です。構成のポアソン比の違いによって生成される垂直応力は、RVE 全体で統合された場合は自己平衡化しますが、1 つの構成で統合された場合には自己平衡化しません。したがって、構成の平均応力状態は、外部のメカニカル荷重により発生した垂直応力、および構成間のポアソン比の相互作用によって発生した垂直応力どちらも保持します。
= 0)。これは、構成材料間のポアソン比の相互作用の直接的な結果です。構成のポアソン比の違いによって生成される垂直応力は、RVE 全体で統合された場合は自己平衡化しますが、1 つの構成で統合された場合には自己平衡化しません。したがって、構成の平均応力状態は、外部のメカニカル荷重により発生した垂直応力、および構成間のポアソン比の相互作用によって発生した垂直応力どちらも保持します。
- 拘束されていない複合材料が、均一な温度変化に影響を受ける場合、構成の熱膨張係数の違いは、RVE 全体で統合された場合は自己平衡化熱応力を発生させますが、1 つの構成で統合された場合には自己平衡化は発生しません。この例では、複合材料の平均応力状態は、一様にゼロです(σc = 0)。ただし、構成の平均応力状態で三軸です(つまり、
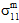 ≠ 0、
≠ 0、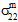 ≠ 0、
≠ 0、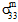 ≠ 0、
≠ 0、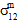 =
= 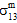 =
= 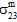 = 0、および
= 0、および 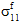 ≠ 0、
≠ 0、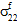 ≠ 0、
≠ 0、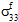 ≠ 0、
≠ 0、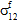 =
= 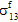 =
= 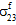 = 0)。
= 0)。
- 一方向繊維強化複合材料は直交異方性(または横等方性)であり、その結果として垂直応力とせん断応力の結合は発生しません。一般的に、複合材料でせん断応力は 2 つの異なる方法で生成されます。第 1 に外部から適用されたメカニカル荷重によって、複合材料にせん断応力が生成されます。これらのせん断応力は自己平衡化しません。したがって、複合材料の平均応力状態(σc)、および構成の平均応力状態(σf および σm)には、これらのせん断応力の測定が含まれています。第 2 に、RVE 内で空間的変化(偏微分方程式のとおり)を示す垂直応力が存在する場合に、ローカルの平衡を維持するために自己平衡化せん断応力場が生成されます。これらのせん断応力は、実際、RVE 内の個別の構成材料内で自己平衡化します。したがって、複合材料の平均応力状態(σc)と構成の平均応力状態 (σf および σm)のいずれにも、これらの自己平衡化せん断応力の測定は含まれていません。
一般的に、実際のマイクロメカニカル応力場 σij(x,y,z)が、個別の構成材料とその材料の接触部分の損傷の進展と破損を発生させると受け入れられていますが、実際のマイクロメカニカル応力場を直接活用するモデルの開発は、圧倒的に複雑で計算が困難な定理です。多重連続体理論では、構成の平均応力状態の概念に焦点を当て、実際のマイクロメカニカル応力場 σij(x,y,z)がミクロ構造内の各構成材料で体積が平均化されます。ただし、構造レベル解析で構成の平均応力状態を効果的に使用するには、構成の平均応力状態の非常に効率的な計算方法を開発することが非常に重要です。実用的な理由で、複合材料構造の構造レベル解析は、複合材料の平均応力状態で定式化されます。したがって、構成の平均応力状態を使用するには、複合材料の平均応力状態を構成の平均応力状態に分解する方法が必要です。MCT 分解と呼ばれるこのプロセスについては、次のセクションで説明します。