構成の平均応力状態を使用して、損傷の開始を独立して識別します。
エネルギー ベースの材料劣化スキームでは、Helius PFA は構成の平均応力状態を使用して、母材構成と繊維構成における損傷の開始を独立して識別します。母材と繊維の損傷開始基準は、すでに説明した構成破損基準と同じです(「母材の構成破損基準」および「繊維の構成破損基準」を参照)。損傷が母材または繊維構成内で開始すると、適切なスカラー損傷変数(母材の場合は D m 、繊維の場合は D f )が、0 から単一性まで進展を開始します。損傷変数(D m および D f )は、以下に示すさまざまな複合ヤング率の剛性低減係数として使用されます。
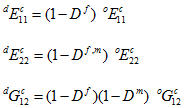
上の損傷複合ヤング率の式では、先行する上付き文字が d の場合は、量が劣化した(または損傷した)量であることを意味し、o の場合は、量が元の(損傷していない)量であることを意味します。 上の方程式では、Df,m は、Dm > 0 の場合は Dm を表すものと理解されます。それ以外の場合、Df,m は Df を表すものと理解されます。
損傷したせん断弾性係数が Dm と Df の両方にどのように依存するかに注意してください。これによって、両方の構成が破損した場合、せん断弾性係数は非線形に劣化します。これは、劣化に対して狭義の減少関数を強制し、エネルギーの損失が常にプラスになるようにします。
1 つまたは両方の構成材料に対して損傷の開始が発生したら、材料が示す可能性のあるひずみ状態に適用可能な構成障害の進展の式が必要です。この目的のための現実的な方法は、それぞれの構成(繊維と母材)に対して適切な応力およびひずみの有効なスカラー計測を使用することです。母材構成内で損傷の進展を予測するため、有効な応力およびひずみを次のように定義します。
母材に対する有効な応力: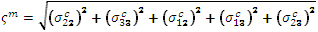 
母材に対する有効なひずみ: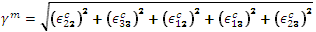 
繊維構成内で損傷の進展を予測するため、有効な応力およびひずみを次のように定義します。
繊維に対する有効な応力: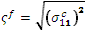 
繊維に対する有効なひずみ: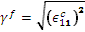 
強調すべきことは、これらの有効な母材および繊維の値は複合材料の平均応力およびひずみ要素から直接計算され、MCT 分解に頼る必要がないということです。
構成損傷変数の進展は、以下に示すようにこれらの有効なひずみに関連して表現されます。
Df は繊維損傷変数(0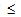
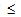Df1)で、以下により計算されます。
ここで、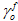
は損傷開始時点での 
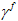の値で、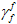
は材料が完全に劣化したとき(剛性がゼロに達したとき)の 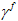の値です。
Dm は母材損傷変数(0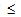Dm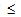1)で、以下により計算されます。
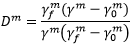
ここで、
は損傷開始時点での 
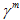の値で、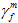
は材料が完全に劣化したとき(剛性がゼロに達したとき)の 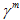の値です。
ここであらためて強調すべきことは、完全に劣化した材料のエネルギー損失は 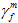および 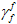に正比例するということです。したがって、以下によって与えられるように、 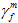および 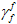が要素サイズに比例することでメッシュの感度が緩和されます。
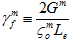
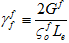
ここで、Gm と Gf は、母材構成と繊維構成がその完全に劣化した状態に達したときのそれぞれの複合エネルギー密度の損失です。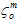
と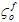 
はそれぞれ母材および繊維の損傷開始時の有効応力です。また、Le は有効な要素長さです。
個別の間隔パーティショニング
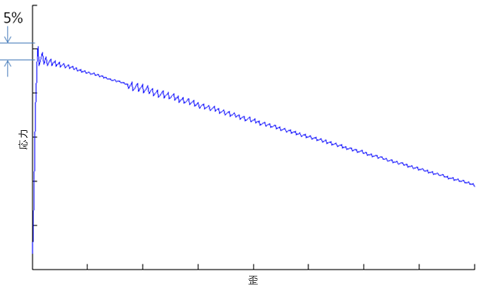
Helius PFA のエネルギーベースの損傷フィーチャは、以下に示すように、複合要素を線形に劣化させるときに複数の個別の間隔を使用します。各間隔は、特定の間隔での複合材料の応答を定義するセカント係数を使用します。エネルギーの合計が二等辺三角形に似た形を表す問題については、複合材料の応答が間隔内に正確にキャプチャされます。
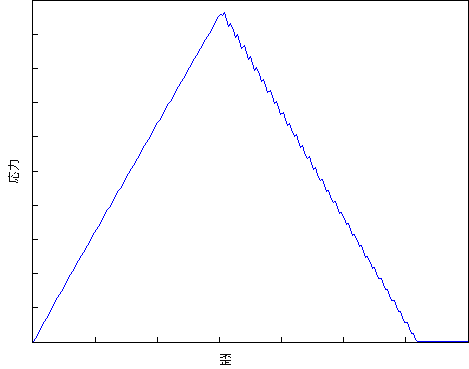
エネルギーの合計が非常に歪んだ三角形を表す解析の場合、以下に示すように、間隔パーティショニングでは初期のひずみレベルでの複合材料の線形ソフトニングが正確にキャプチャされません。これは、問題を最も迅速かつ確実に収束させるために使用される間隔の数が原因です。具体的には、破損付近のひずみレベルでの応力割線間隔は高い剛性を維持しており、複合材料の応力状態を間違って示すことがあります。最終の有効ひずみが最初の有効ひずみの 100 倍を超える線形劣化曲線を定義する解析の場合は、オートデスクにサポートを依頼してください。
