初期の破断エネルギーの値を決定する

複合材料で放出されるエネルギーを決定します。

Helius PFA でエネルギーベースの劣化(EBD)機能を使用するには、2 つの値が必要です。

1. G^m - 母材破損後に、複合材料で散逸されるエネルギーの合計です(ユーザ材料定数 12)。
2. G^f - 繊維破損後に、複合材料で散逸されるエネルギーの合計です(ユーザ材料定数 14)。

Helius PFA の EBD 機能は、以下に示すように線形劣化モデルを使用します。

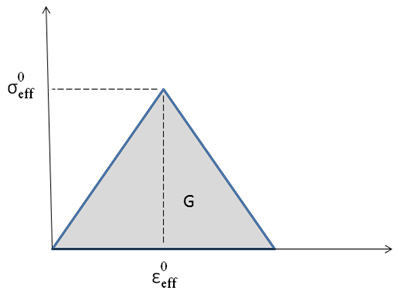
上の図から、要素の総エネルギーは次のように表現することができます。

ここで、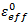 は母材/繊維破損の複合材料の有効なひずみ値、 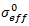は母材/繊維破損の複合材料の有効な応力、V_e は要素の体積です。

母材構成の場合、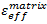 は次のように表現されます。

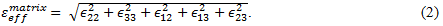
繊維構成の場合、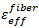 は次のように表現されます。

母材構成の有効な応力、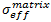 は同様に次のように表現されます。

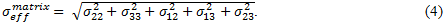
繊維構成の有効な応力、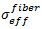 は同様に次のように表現されます。

式 2～5 では、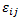 と 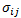の値はすべて複合材料の単層ひずみと応力です。破損時の損失エネルギーを見積もるには、複合材料の単層ひずみと応力の値を、破損ひずみと破損応力の値に置き換えることができます。IM7/8552 では次の強度(破損応力)値を利用できます。

1. ⁺S₁₁ = 362 ksi
2. ⁺S₂₂ = ⁺S₃₃ = 9.29 ksi
3. S₁₂ = S₁₃ = 13.2 ksi
4. S₂₃ = 13.8 ksi

利用可能な破損ひずみ値がない場合、単純化したフックの法則を使用して破損ひずみを決定することができます。この場合、破損の前の材料応答はほぼ線形であると想定します。

IM7/8552 では次の弾性ヤング率(E)を利用できます。

1. E₁₁ = 20 Msi
2. E₂₂ = E₃₃ = 1.42 Msi
3. G₁₂ = G₁₃ = 0.669 Msi
4. G₂₃ = 0.0475 Msi

IM7/8552 に対して提供される材料特性を使用し、式 6 を式 2 および 3 に代入すると、破損時の IM7/8552 に対する以下の有効なひずみ値および応力値を計算することができます。

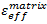1. = 0.0413
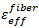2. = 0.0181
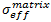3. = 26.7 ksi
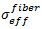4. = 362 ksi

この例の問題は、要素の体積を持たない 2D シェル要素を使用して作成されています。この値は、要素の領域に積層厚さを掛けることで見積もることができます。要素の領域は、有限要素モデルに割り当てられたメッシュのグローバル シード サイズを 2 乗することで簡単に決定することができます。この例では、0.05 インチのグローバル シード サイズが OHT モデルに割り当てられました。OHT に使用される積層は 16 層で、各層の厚さは 0.0072 インチです。これらの値を使用して、0.0115 インチ³ の要素体積が計算されます。

要素の体積、母材の有効なひずみ/応力、繊維の有効なひずみ/応力を式 1 に入力すると、次のエネルギー値が計算されます。

• G^m = 12.7 in.-lb.
• G^f = 75.5 in.-lb.

エネルギーベースの劣化を使用する時にユーザ材料定数 12 および 14 に入力されるのは、これらの 2 つの値です。