このトピックにおいては、連成方程式を解く場合に使用される手法と関連する専門用語を定義します。
Autodesk® CFD の分離型ソルバーによる演算手順を示します。
- ジオメトリ、境界条件、解析データの読込
- データ構造の作成
- X 方向運動量方程式の計算
- Y 方向運動量方程式の計算
- Z 方向運動量方程式の計算
- 圧力方程式の計算と流速の修正
- エネルギー方程式の計算
- 乱流運動エネルギー方程式の計算
- 乱流エネルギー消失率方程式の計算
- 収束の確認(ステップ 3 に戻る)
- 出力計算の実行
- データの書込
- 終了
それぞれの支配方程式が別々に解かれることに注意してください。また、温度変化のない解析の場合、エネルギー方程式の計算が省略されます。同様に、層流解析では乱流方程式の計算が省略されます。
その他に、V流速方程式およびW流速方程式は、ごく短時間しか矢印によって指示されないことにも気付くでしょう。運動量方程式の類似性のため、U流速方程式のみをセットアップし、他の2つの運動量方程式に対してその設定を適用できる場合が多くあります。
グローバル反復
支配方程式は非線形であるため、繰り返し解かれなければなりません。Picard法または 逐次代入法が使用されます。この方式において、支配方程式には解析変数(U, V, W, P, T, K,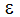 
)が代入されます。この支配方程式は次の値に対して解かれ、その後、さらにこの解かれた値はその次のステップの推定値として利用されます。全体の繰返し計算は、図1の破線の枠で囲まれた部分です。Autodesk® CFD は、全体の反復計算を一定回数実行するか、収束判定基準のチェックを行い、一定回数または一定基準に達すると終了します。収束の判断基準は、特定の変数の残差ノルムが達しなければならないレベルです。残差ノルムについては、以下の節において定義します。前述したように、解の収束の評価には、圧力方程式を使用することを推奨します。
収束/残差/残差ノルム
上述した全体の繰返し計算の進行とともに、求められる値は正確な解に近付いていく、あるいは収束していきます。正確な解は既知の値ではないため、収束の基準を見出す必要があります。解の収束を確認するために使用できるパラメータはいくつも存在します。数々のパラメータが試されていますが、どのような状況に対しても最適である値は存在しません。しかし、最も広範囲の問題について最も多くの情報を与えるパラメータは、残差ノルムであることが確認されています。
まず最初に残差を定義します。支配方程式が離散化されると、支配方程式は、U, V, W, P, T, K, 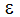などの従属変数に関する一連の代数方程式となります。これらの変数のそれぞれについて、解析モデル内の各有限要素に関する方程式が存在します。節点iにおける変数 
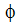に関する典型的な代数方程式は、次のように表すことができます。
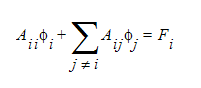
ここで、Aijは、指定方程式の移流項および拡散項の離散化によって得られる代数行列、Fiは離散化されたソース項です。この方程式の残差は、以下のように定義されます。
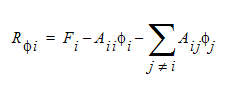
ここで、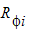
は、節点iにおける節点残差です。
解が収束しつつある場合、残差は、分離型ソルバーの繰り返し計算または全体の繰返し計算の進行とともに小さくなっていきます。それぞれの全体繰返し計算後に節点残差がプロットされるのではなく、節点残差のノルムが求められます。ノルムによって、効果的に全ての節点残差が1つの数へと統合されます。
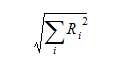
解が収束していく場合、節点残差と同様に、残差のノルムも小さくなっていきます。解の収束のインジケータとして、Autodesk® CFD がステータス ファイルに出力し、収束モニタ ウィンドウ上にプロット表示するのが、節点残差のノルムです。
収束評価の他のインジケーターとして、従属変数の最小値・最大値・平均値を確認する方法があります。これらのパラメータは全て、1つの値に漸近する必要があります。そのようになる場合、ソルバーにおける値の大きな変化はなくなり、解は収束したと考えられます。最終的な収束の確認方法は、ポストプロセッサーにより、異なる繰返し計算ステップの解を比較することです。異なる2つの繰返し計算ステップのそれぞれを比較し、結果に大きな変化が見られない場合、目的に対して十分に解が収束していると考えられます。
残差と圧力 - 速度カップリング
Autodesk® CFD での圧力と速度の結合には、シンプルなアプローチを使用します。
運動量方程式は、u = u_hat - K_u * dpdx, v = v_hat - K_v * dpdy, w = w_hat - K_w * dpdz として表すことができます。
これらの方程式を連続方程式に入れると、ポアソン圧力方程式、DEL(K DEL P ) = S_p が生成されます。解析対象の圧力は連続性を満たしているため(重み関数の手法で)、連続方程式の残差はゼロになります。圧力残差は、圧力マトリックスの残差、r[I] - S_p[I] - A_ij * P[j] として計算することができます。ソルバーは、圧力方程式を解析する前に、圧力残差として r[I] の L-2 ノルムを取ります(収束モニタに表示されるように)。