사출 성형 부품의 경우 부품이 금형에서 구속됩니다. 사출 성형 부품의 고화 중에는 고화된 레이어의 수축이 방지됩니다. 부품이 금형에서 취출되면 이러한 잔류 응력이 수축 변형의 형식으로 제거됩니다.
금형에 있는 동안 고화된 레이어의 수축은 몇 가지 메커니즘으로 방지할 수 있습니다. 금형 벽에 부착하면 솔리드 레이어(적어도 외부 스킨)의 이동이 제한됩니다. 새로 형성된 솔리드 표면은 용융 압력의 신장력에 의해 고정된 상태를 유지합니다. 또한 형상 구속조건도 중요한 역할을 합니다. 시뮬레이션에서 부품은 금형에 완전히 구속된 것으로 가정됩니다. 어떠한 부품-금형 분리 및 인-몰드 수축도 고려되지 않습니다.
캐비티 내 잔류 응력은 고화 중에 형성됩니다. 구속조건이 지정된 급랭의 특성으로 인해 잔류 응력 분배는 주로 고화층 성장과 함께 다양한 압력 이력에 의해 결정됩니다. 부품이 금형에서 취출되면 이러한 잔류 응력이 수축 변형의 형식으로 제거됩니다. 캐비티 내 잔류 응력과 동일한 초기 변형이 균등한 경우 부품이 변형 및 성형 후 잔류 응력 없이 균등하게 수축됩니다. 변형은 부품 전체의 수축 변동으로 인해 발생합니다.
두 가지 유형의 수축 변동이 고려됩니다.
- 리전 간 수축 변동(수축 효과)
- 일반적으로 벽이 얇은 부품의 경우 이런 형식의 수축 변동은 냉각 효과 및 표면 리전 간 변동으로 인해 주로 발생하는 성형된 부품의 두께 방향 변동으로 분할할 수 있습니다.
- 다른 방향의 수축 변동(배향 효과)
- 평행 수축과 수직 수축 간 차이 및 섬유 배향 분배와 관련된 이방성 재료 속성이 섬유 충전 열가소성 수지 부품 변형의 주요 원인 중 하나입니다.
사출 성형 부품의 수축은 공정 중 재료의 열역학 동작에 따라 달라집니다. 간단한 설명을 위해 고화된 부품의 선형 탄성 동작 및 용융의 순수 점성 동작, 즉 열점탄성 재료 모델을 가정해보겠습니다.
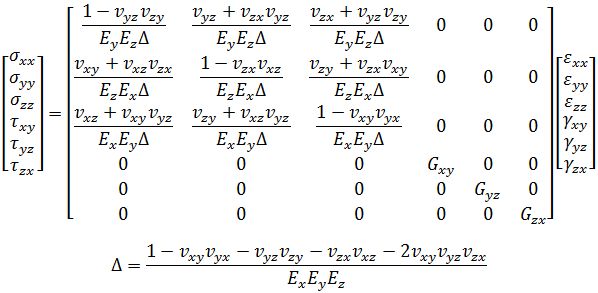
4절점 1차 4면체 요소가 3D 유동 시뮬레이션에 적합합니다. 그러나 1차 4면체 요소가 일반적으로 벽이 얇은 부품이나 복잡한 3차원 부품의 얇은 벽 영역의 변형 해석에 사용되는 경우 심각한 전단 잠금 문제로 인해 구조 반응이 매우 단단해질 수 있습니다[1]. 전단 잠금 또는 기생 전단은 선형 4면체 요소에 대한 선형 변위 필드의 부정확성으로 인해 발생합니다. 이 문제는 면비가 큰 요소에 의해 악화될 수 있습니다. 반면 계산 비용을 낮게 유지해야 하는 경우 면비가 높은 4면체 요소를 피할 수 없습니다. 따라서 1차 4면체 요소는 사출 성형 부품의 얇은 벽 영역에 적합하지 않습니다.
하이브리드 요소 구조는 3D 변형 해석을 위해 설계되었습니다. 4절점 1차 4면체 요소는 3D 솔리드 영역에서 사용되고 10 절점 2차 4면체 요소는 얇은 벽 영역에서 사용됩니다. 천이 5-9 절점 4면체 요소는 얇은 벽 영역과 두꺼운 영역을 연결하는 천이 영역에서 사용됩니다.
금형 경계 구속조건이 해제되면 변형 및 성형된 잔류 응력 결과가 계산됩니다. 모든 변수는 솔루션 계산법에서 시간 0의 초기 구성으로 참조되므로 증분 초기 변형 또는 응력을 자연스럽게 구현할 수 있습니다. 다음 평형 방정식은 시간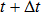 
에, 반복 k = 1, 2, 3, ...에 대해 반복적으로 해석됩니다.
여기서:
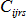은 응력-변형 텐서입니다.
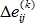및 
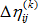은 반복 k에 대한 선형 및 비선형 증분 변형 텐서입니다.
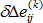및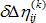 
은 가상 증분 변위에 해당하는 선형 및 비선형 증분 변형 텐서입니다.
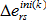은 반복 k에 대한 증분 초기 변형 텐서입니다.
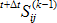은 시간 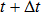에서 반복 (k-1) 이후의 두 번째 Piola-Kirschoff 응력 텐서입니다.
일반적으로 3D 변형 시뮬레이션에는 많은 계산 시간이 필요합니다. 특히 요소 수가 매우 많은 경우와 큰 얇은 벽 리전이 있는 경우에는 더욱 그렇습니다. 효율적인 사전 조절 켤레 구배 반복형 솔버를 구현하여 메모리 요구사항 및 계산 시간을 줄입니다.
참조 문헌:
[1] K.J. Bathe, Finite Element Procedures, Prentice Hall Inc.(1996).
[2] S.G.Advani 및 C.L.Tucker III, The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites, J. Rheol., 31,751-784(1987).
[3] G.P.Tandon 및 G.J.Weng, The Effect of Aspect Ratio of Inclusions on the Elastic Properties of Unidirectional Aligned Composites, Polym. Compos. 5(4),327-333(1984).
[4] R.A.Schapery, Thermal Expansion Coefficients of Composite Materials Based on Energy Principles. J. Compos. Mater., 2, No.3, 380-404, (1968).