냉각은 True 3D 금형 냉각 해석 제품입니다. 냉각은 BEM(Boundary Element Method)에서 개발된 수치 방법을 사용합니다. 물리적 관점에서 BEM은 솔루션 중 모든 경계를 열 소스(열 취득/손실)로 처리합니다.
금형의 온도는 모든 소스의 영향을 결합하여 결정됩니다.
3D 금형의 평형 온도 필드는 라플라스 방정식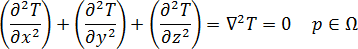 
로 표현할 수 있습니다.
여기서:
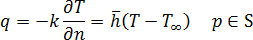
로 통합된 해당 영역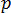
의 특정 지점을 참조합니다.
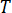는 온도입니다. 
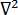은 라플라스 연산자입니다. 
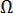는 금형의 표면적 및 내부를 나타냅니다.
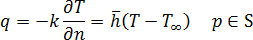
로 통합된 해당 영역
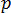의 특정 지점을 참조합니다. 여기서:
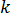는 금형 재료의 열전도 계수입니다. 
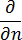는 금형 경계면의 바깥쪽 법선 파생을 나타냅니다. 
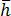는 금형 경계면의 해당 열전달 계수입니다. 
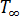는 주변 환경의 해당 온도입니다. 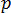- 는 특정 점을 나타냅니다.
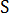는 금형 면(경계)입니다.
BEM이 모든 경계 조건을 금형 온도 필드의 솔루션에 적용하는 방법을 이해하기 위해 가중치 적용 잔류 표현식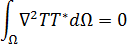 
에서 시작하겠습니다.
여기서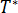 
는 가중치 함수입니다.
녹색의 두 번째 ID를 사용하여 방정식 3을 다음 형식으로 변환할 수 있습니다.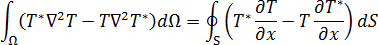
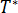를 방정식 1의 기본해로 선택하며 
로 정의됩니다.
여기서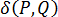 
는 디랙 델타 함수입니다. 3D 금형의 경우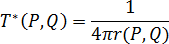 
로 설명할 수 있습니다.
여기서:
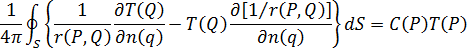
로 단순화할 수 있습니다.
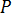및 
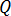는 공간의 두 점이고 
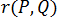는 두 점 간의 거리를 나타냅니다.
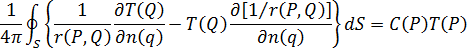
로 단순화할 수 있습니다.
여기서:
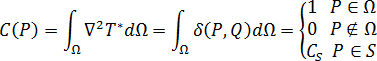및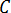 
는 내부 입체각에 비례하는 상수입니다.
이제 방정식 7에는 경계 통합만 있습니다. 따라서 모든 금형 면 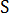를 
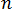개 요소로 분할할 경우 온도 및 온도 구배가 각 경계 요소에 대해 일정하면 방정식 7을
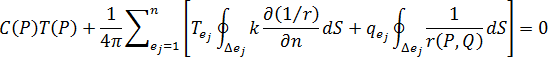
형식으로 분리할 수 있습니다. 여기서
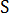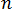를 개 요소로 분할할 경우 온도 및 온도 구배가 각 경계 요소에 대해 일정하면 방정식 7을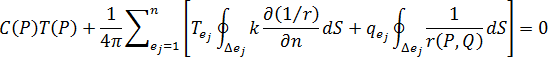 형식으로 분리할 수 있습니다. 여기서
는 특정 요소입니다. 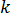- 는 금형 재료의 열전도 계수입니다.
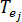는 요소의 온도입니다.
요소에서 점 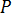에 대한 온도의 영향 강도를 나타내는 온도 영향 항(또는 소위 H 항)은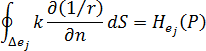 
표현식으로 지정됩니다.
요소에서 점 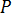에 대한 열 플럭스 입력의 영향 강도를 나타내는 열 플럭스 영향 항(또는 소위 G 항)은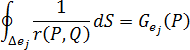 
표현식으로 지정됩니다.
가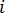 
요소의 중심이라고 가정합니다. 방정식 9에서 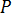를 로 대체할 경우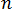 선형 방정식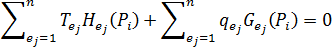 
을 구할 수 있습니다.