불안정 변형으로 인해 성분의 좌굴이 발생합니다. 총 변형에 대한 세 가지 각 수축 변동의 기여도가 더 이상 선형으로 가정되지 않을 수 있습니다.
이 경우 소위 감도 해석이 사용됩니다. 이 기능은 미드플레인 해석 기술에만 사용할 수 있습니다.
감도 해석의 목표는 알려진 수축 변화에 대한 하중 계수의 변화를 확인하는 것입니다. 하중 계수는 실제 적용된 하중(수축 해석의 경우 제품 내부의 하중임)의 어떤 계수에서 제품 변형이 불안정해져 좌굴이 발생하는지를 나타냅니다. 1보다 작은 하중 계수는 실제 하중이 충분하여 제품의 좌굴이 발생함을 나타냅니다. 1보다 큰 하중 계수는 좌굴의 시작이 실제 하중보다 높은 하중 크기인 것으로 확인되면 변형이 안정적임을 나타냅니다.
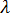는 이러한 성분의 함수, 즉 다음과 같이 간주됩니다.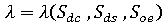 
변형 문제를 해결하려면 하중 계수를 높이기 위해, 즉 변형을 안정적으로 만들기 위해 변경할 성분을 알고 있어야 합니다. 이렇게 하는 한 가지 방법은 각 성분에 대해 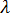의 부분 파생을 사용하는 것입니다. 안타깝게도 이 방법은 성분과 관련된 알려진 함수 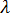가 없기 때문에 해석적으로 수행할 수 없습니다. 대신 부분 파생의 근사치가 계산됩니다.
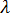라고 가정합니다. 이제 수축 성분 중 하나를 약간씩, 즉 
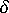만큼 증가하여 새로운 총 수축 S'를 제공합니다. 예를 들어 수축 효과 성분을 늘리면 다음과 같이 됩니다.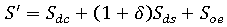 
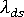를 얻으면 다음과 같이 수축 효과 성분에 대한 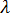파생물의 근사치가 계산됩니다.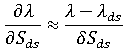 
이는 아래 이미지와 같이 표시됩니다.
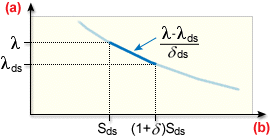
수축 함수로 사용된 하중 계수
.(a) 하중 계수, (b) 수축
값(1 + 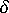)을 프로그램 입력인 감도 계수라고 합니다.
위의 값은 한 요소에 대해서만 유지됩니다. 실제 제품의 경우 각 개별 요소에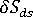 
값이 있습니다. 이를 처리하기 위해 다양한 요소 변화가 수축 변화의 단일 측정과 결합됩니다. 이러한 변화의 놈은 요소 수축에서 사용되어 단일 값을 얻고, 해석 로그에서 수축 변화 놈으로 보고됩니다.
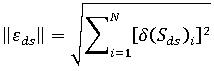
여기서 N은 모델에 있는 요소의 수입니다.
마찬가지로 냉각 효과 및 배향 효과 변량에 대한 하중 계수의 감도가 각각 계산됩니다.
그러면 수축 변화 놈은 각 요소에서 수축 변화 제곱의 합이 되고 변형 좌굴의 감도 해석에 사용됩니다.