적절한 결정화 형태 속성 데이터에서 열가소성 수지 반결정 재료를 사용하는 경우 결정화 해석을 수행하는 옵션이 구현되었습니다.
결정화 특성 모델링
유동 향상 결정화, 전단 유동 도중 및 이후 반결정 재료의 유동 유도 형태 변경을 비롯한 결정화 특성의 모델링이 열가소성 수지 유동 솔버에서 구현되었습니다.
결정 성장률은 재료 유동의 영향을 크게 받지 않는 것으로 확인되었습니다. 따라서 성장률은 온도에 따라서만 달라지고 Hoffman-Lauritzen 이론[1]을 따르는 것으로 가정됩니다.
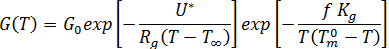
여기에서 각 항목은 다음과 같습니다.
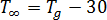 및
및 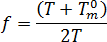 .
. 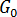 및
및 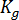 은 정지 조건에 따라 결정될 수 있는 재료 등급별 상수입니다.
은 정지 조건에 따라 결정될 수 있는 재료 등급별 상수입니다. 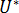 은 동작의 활성화 에너지,
은 동작의 활성화 에너지, 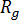 은 가스 상수,
은 가스 상수, 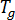 은 유리 천이 온도,
은 유리 천이 온도, 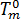 은 압력에 따라서만 달라지는 것으로 가정되는 재료 등급별 평형 용융 온도입니다. 압력 종속성[2]을 설명하기 위해 선형 함수가 선택되어 있습니다.
은 압력에 따라서만 달라지는 것으로 가정되는 재료 등급별 평형 용융 온도입니다. 압력 종속성[2]을 설명하기 위해 선형 함수가 선택되어 있습니다.
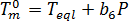
여기서 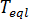 은 평형 용융 온도,
은 평형 용융 온도, 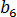 은 재료에 대한 PVT 모델의 등급별 상수, P는 압력입니다.
은 재료에 대한 PVT 모델의 등급별 상수, P는 압력입니다.
핵 생성은 다음으로 표현됩니다.
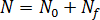
여기서 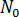 은 정지 상태의 활성화된 핵 수이고,
은 정지 상태의 활성화된 핵 수이고,  은 유동에 의해 활성화된 핵 수입니다.
은 유동에 의해 활성화된 핵 수입니다.
정지 상태의 활성화된 핵 수는 과냉각 온도의 고유 함수(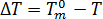 )로 가정되며, 다음에 의해 설명됩니다[3].
)로 가정되며, 다음에 의해 설명됩니다[3].
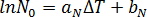
여기서 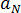 및
및 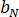 은 재료 등급별 상수입니다.
은 재료 등급별 상수입니다.
결정화에 대한 유동의 효과는 초과 자유 에너지와 유동 유도 배향을 결정화 특성과 연결하여 고려합니다. 유동 유도 핵 수는 다음과 같은 미분 방정식으로 지정합니다.
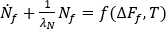
여기에서 각 항목은 다음과 같습니다.
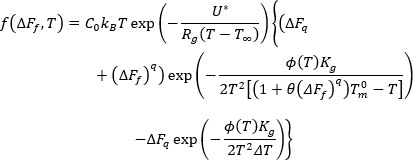
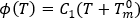 )이고,
)이고,
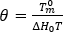
결정화도 개발로 인해 점도가 증가하고 결국에는 고화도 증가하게 됩니다. 시뮬레이션에서는 향상 계수를 적용하여 점도에 대한 결정화도의 효과를 설명했습니다[4].
 <
< 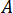 인 경우
인 경우 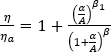
여기서 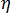 은 전체 시스템의 점도,
은 전체 시스템의 점도, 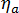 는 비결정성 단계의 점도,
는 비결정성 단계의 점도, 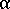 은 상대 결정화도입니다.
은 상대 결정화도입니다.
참조 문헌
[1]S.I. Lauritzen and J. D. Hoffman, ''Theory of formation of polymer crystals with folded chains in dilute solution,'' J. Res. Natl. Bur. Stand. 64A, 73-102 (1960)
[2] R. Fulchiron, E. Koscher, G. Poutot, D. Delaunay, and G. Regnier, ''Analysis of the pressure effect on the crystallization kinetics: dilatometric measurements and thermal gradient modelling,'' J. Macromol. Sci., Phys. 40, 297-314 (2001)
[3] E. Koscher and R. Fulchiron, ''Influence of shear on polypropylene crystallization: morphology development and kinetics,'' Polymer 43, 6931-6942 (2002)
[4] R. Zheng and P. K. Kennedy, "A model for post-flow induced crystallization: General equations and predictions", J. Rheol., 48(4), 823-842 (2004)