섬유 배향은 기계적(탄성) 강도 및 성형 부품의 강성을 결정하는 주요 요소 중 하나입니다.
부품의 섬유 배향 분포를 알고 있는 경우 짧은 섬유 컴포지트의 기계적 속성을 예측하기 위해 개발되었습니다.
기계적 속성을 계산하려면 모든 이론에서 다음과 같은 2단계 절차를 따릅니다.
- 단일 지향성 짧은 섬유 강화 재료의 속성이 예측됩니다.
- 그런 다음 섬유 배향 분포에 따라 이러한 속성의 평균을 구합니다.
따라서 이 방법은 섬유 길이 및 섬유 배향의 영향을 독립적으로 고려합니다.
Tandon-Weng 모델은 등방성 매트릭스에 대한 컴포지트 재료의 단일 지향성 기계적 속성 계산의 기초로 사용됩니다. Autodesk Moldflow Insight 구현에서도 Tandon-Weng 모델의 푸아송 비 계산에 대한 Tucker/Liang의 처리를 고려합니다.
해석에 대한 입력으로 필요한 섬유 및 고분자 속성은 다음과 같습니다.
-
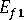 (섬유의 세로 계수)
(섬유의 세로 계수)
-
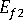 (섬유의 가로 계수)
(섬유의 가로 계수)
-
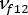 (섬유의 세로 푸아송 비)
(섬유의 세로 푸아송 비)
-
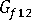 (섬유의 세로 전단 계수)
(섬유의 세로 전단 계수)
-
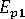 (고분자의 세로 계수)
(고분자의 세로 계수)
-
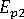 (고분자의 가로 계수)
(고분자의 가로 계수)
-
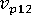 (고분자의 세로 푸아송 비)
(고분자의 세로 푸아송 비)
-
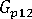 (고분자의 세로 전단 계수)
(고분자의 세로 전단 계수)
-
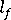 (평균 섬유 길이)
(평균 섬유 길이)
-
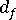 (평균 섬유 지름)
(평균 섬유 지름)
-
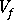 (섬유의 체적 분율)
(섬유의 체적 분율)
컴포지트 재료의 각 요소에 대해 다음과 같은 기본적인 기계적 속성이 도출됩니다.
-
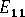 (세로 계수)
(세로 계수)
-
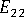 (가로 계수)
(가로 계수)
-
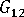 (평면 전단 계수)
(평면 전단 계수)
-
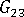 (평면 이탈 전단 계수)
(평면 이탈 전단 계수)
-
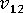 (평면 푸아송 비)
(평면 푸아송 비)
-
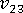 (평면 이탈 푸아송 비)
(평면 이탈 푸아송 비)
세로 및 가로 계수
Tandon-Weng 모델에서는 짧은 섬유 강화 컴포지트를 유한 탄성 고분자 매트릭스에 내장된 단일 지향성 정렬 타원체 함유물의 특수한 사례로 처리합니다.
단일 축 정렬 시스템의 세로 계수는 다음과 같이 기록할 수 있습니다.
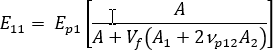
여기서 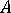 ,
, 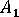 그리고
그리고 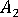 는 Tandon Weng 논문의 변수와 관련된 변수입니다.
는 Tandon Weng 논문의 변수와 관련된 변수입니다.
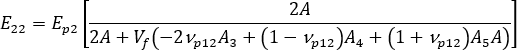
여기에서 각 항목은 다음과 같습니다. 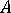 ,
, 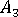 ,
, 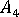 및
및 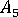 는 Tandon-Weng의 논문에 나오는 것과 관련된 매개변수입니다.
는 Tandon-Weng의 논문에 나오는 것과 관련된 매개변수입니다.
전단 계수 및 푸아송 비
단일 축 정렬 시스템의 세로 전단 계수는 다음과 같이 작성될 수 있습니다.
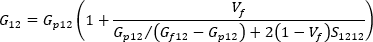
단일 축 정렬 시스템의 가로 전단 계수는 다음과 같이 작성될 수 있습니다.
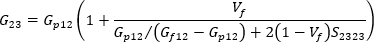
여기서 S1212 및2323은 Tandon-Weng의 논문에서 발표된 해석 솔루션인 Eshelby 텐서의 해당 구성요소입니다.
단일 축 정렬 시스템의 평면 푸아송 비는 다음과 같이 작성될 수 있습니다.
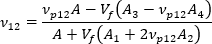
단일 축 정렬 시스템의 평면 이탈 푸아송 비는 컴포지트 계수에서 다음과 같이 명시적으로 계산될 수 있습니다.