使用 KTF 检查织物复合材料。
在织物层中,疲劳期间出现的基体支架微观裂纹对层的承载响应的影响非常微不足道 [22-24]。因此,我们会忽略由基体支架中微观裂纹引起的任何失效,因为它在织物层的疲劳过程中不起主要作用。
有建议指出,后续脱层通过疲劳载荷期间彼此牵引磨损的摩擦作用而对材料滞后产生显著影响 [25-26]。还有建议指出,这些脱层具有解耦牵引的能力,从而允许在疲劳载荷期间重新分布应力。为了简单起见,我们暂时忽略后续脱层对疲劳求解的影响。我们还假定织物微观结构的最终失效经由垂直于纤维方向的基体裂纹开始。一旦基体失效开始出现在牵引束内,紧接着将出现牵引的最终失效。
上面列出的用于理想化疲劳失效过程的假设现在可作为以下事件序列提出:
- 在疲劳载荷过程中束内基体成分中的横向裂纹
- 在疲劳载荷过程中导致纤维失效的基体成分中的纵向裂纹
最后,由于疲劳载荷而使得实验数据很少报告束中出现的横向裂纹。仅报告的信息是在应用的应力级别上失效出现前的循环次数。因此,我们假定仅纵向裂纹会对平织材料的疲劳失效产生影响。尽管这似乎是一种粗略的简化,但是织物复合材料专为束内横向裂纹而设计。牵引的架构提供了层的任何平面内方向上的“纤维”响应。
同轴
平织层平面内的任何载荷最终会导致纤维翘曲形式的严重失效事件。我们前面已提到过,因纵向裂纹而在疲劳载荷过程中出现的彻底失效来自于桥接纤维的基体成分内裂纹。在出现纵向裂纹不久之后,纤维失效,由于纤维成分内存在大量应力集中。
理论上,针对单向材料开发的同轴有效应力同样可应用于织物微观结构。但是,使用上一页上显示的体积平均应力会“过滤出”自平衡应力。在平织复合材料中,这意味着纯剪切载荷将导致仅应力的剪切分量存在于基体成分中,因为其他应力分量是自平衡的。纯剪切载荷不会导致任何有效应力出现最终疲劳失效,即使证实纯剪切载荷会导致织物层出现疲劳失效也是如此 [22]。因此,我们将平织复合材料的 Eq. 44 修改为:

其中:

Eq. 47 可进行修改,以生成失效索引而非有效应力,具体形式如下:

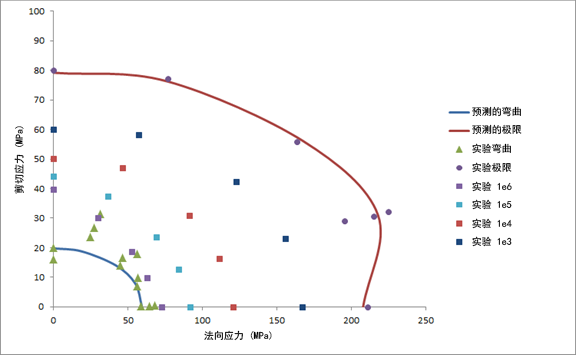
A i 的值由三项复合静态失效测试确定:纵向拉伸、纵向压缩和平面内剪切。显示在 Eq. 47 中的失效准则已根据实验数据进行验证,而结果标记为“预测的极限”,如下所示。