Puck 准则

Puck 准则标识单向复合材料中的纤维失效和纤维之间的失效。

Puck 准则还将纤维失效分为两个不同的物理模式。要使用 Puck 失效准则，则必须指定两部分信息。

复合材料类型：必须指定碳纤维增强聚合物 (CFRP) 或玻璃纤维增强聚合物 (GFRP)。
选定的纤维特性：纵向模量、纵向泊松比。

纤维失效

Puck 准则识别两种不同模式的纤维失效：第一个是拉伸失效，第二个是压缩的“纤维扭结”失效。拉伸纤维失效准则为

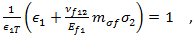
而压缩的“纤维扭结”失效为

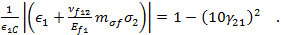
在上面的纤维失效准则中：

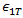
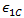
: 复合材料应变分别对应于复合材料纵向拉伸和压缩失效。

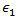
: 复合材料中的单轴应变。

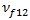
: 纤维的纵向泊松比。

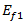
: 纤维的纵向拉伸模量。

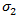
: 复合材料的横向应力。

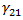
: 复合材料的纵向剪切应变。

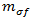
: 旨在捕获纤维和基体中横向应力之间的差异。对于碳纤维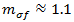，；对于玻璃纤维，。

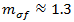在上面的方程中，如果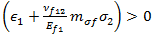，将计算拉伸方程；如果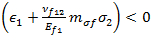，将评估压缩准则。

纤维之间的失效（基体裂纹）

在 Puck 准则中，纤维之间的失效包含任何基体裂纹或纤维/基体脱粘。Puck 准则识别三种不同的纤维之间的失效模式，这些模式分别称为模式 A、B 和 C。这三种纤维之间的失效模式可通过相对于增强纤维的断裂平面取向进行区分。

纤维之间的失效模式 A：

模式 A 对应于 0° 断裂角。如果复合材料中的横向应力大于 0（这表明横向裂纹垂直于横向载荷），则调用该准则。

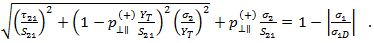
纤维之间的失效模式 B：

模式 B 对应于横向压缩应力（抑制裂纹形成），其纵向剪切应力低于断裂阻力（外加经验常数）。

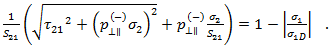
在以下情况下将评估上述准则

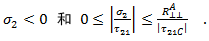
纤维之间的失效模式 C：

模式 C 对应于横向压缩应力（抑制裂纹形成），其纵向剪切应力明显太大，导致倾斜平面到纤维轴上出现断裂。模式 C 的失败准则为

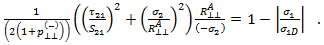
在以下情况下将评估上述准则

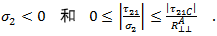
纤维之间的失效准则中使用的系数和术语的描述

接下来介绍：

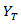
: 复合材料横向拉伸强度。

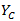
: 横向压缩强度。

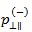
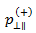
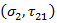: 断裂包络的斜率。

若要在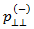和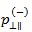之间建立连接，则假定以下关系保持不变

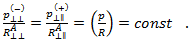
因此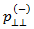，可表示为

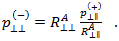
其中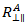假定为与 S₂₁ 相同，这将允许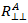表示为

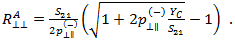
Puck 和 Mannigal (2007) 为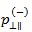和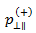提供了以下建议值。

Puck 还将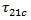定义为

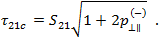
最后，我们必须定义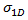。这是复合材料中的“降级”应力，使得各个纤维出现预纤维失效翘曲，进而导致在这些区域中出现微裂纹和脱粘形式的损坏。出于对这种削弱效果的考虑，Puck 通过削弱因子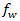降低了断裂阻力 (R)。Puck 为此定义了两个方程。第一个用于广义削弱因子。

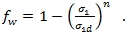
第二个用于提供削弱因子的另一个表达式以使断裂条件同类，还用于提供关于应力的一次表达式。

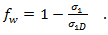
Puck 准则的 Helius PFA 实施仅利用三维应力状态的平面内应力分量。在这种情况下，上述两个方程应为等效表达式，因为在将执行的断裂平面上不存在任何迭代计算。因此，我们可以得出

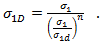
根据 Puck 的建议，Helius PFA 将 n=6 用于指数，并按 1.1X_T 或 -1.1X_C 经验计算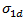，具体取决于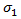的符号。

应当强调的是，Puck 准则的 Helius PFA 实施仅使用三维应力和应变的平面内分量，即 σ₁₃、σ₂₃、σ₃₃，它们不用于计算材料失效。