基于能量的损坏演变简介

查看基于能量的损坏演变公式。

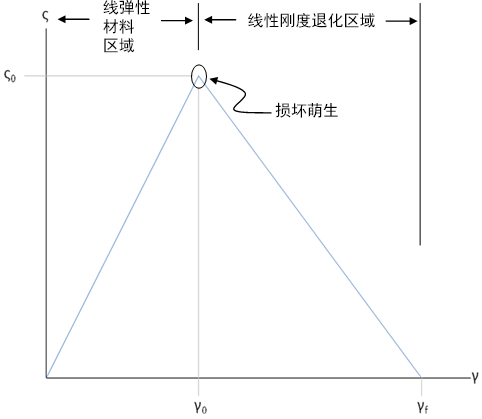
最简单的本构关系（即允许要控制的材料降解率）是由线性弹性区域后跟线性刚度降级区域组成的双线性定律，如图所示。在此图中，ς₀ 表示失效开始时复合应力的有效测量。γ₀ 表示失效开始时复合应变的有效测量。γ_f 表示以下情形下复合应变的有效测量：损坏已完全演变并且材料刚度已完全降为零，以阻止材料承载任何载荷。

现在，考虑已完全降级的单元体积 V _e 所耗散的总能量 G。对于上面所示的简单本构关系，此耗散的总能量可表示为

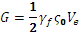
其中 γ_f 是测量的有效应变的最终值，而 ς₀ 是失效开始时测量的有效应力值。

缓解与渐进式失效结果相关联的网格敏感度在于，使总能量耗散保持恒定，不考虑单元大小。该恒定能量耗散可通过适当地控制 ς₀ 或 γ_f 作为单元大小的函数获得。在失效分析中，更改值 ς₀ 将有效地更改复合材料视为失效时的应力。这在直观上并没有吸引力，因此最为直接的选择是更改 γ_f，以便能量 G 对各种单元大小守恒

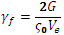
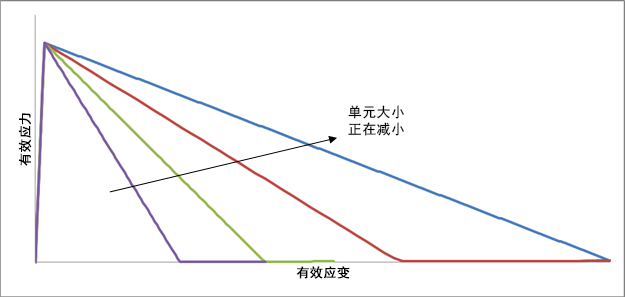
下图显示了在单元大小更改时，针对 G 的单个可接受值所获得的生成本构定律系列。